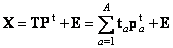Анализ главных компонент (Principal Component Analysis, PCA)

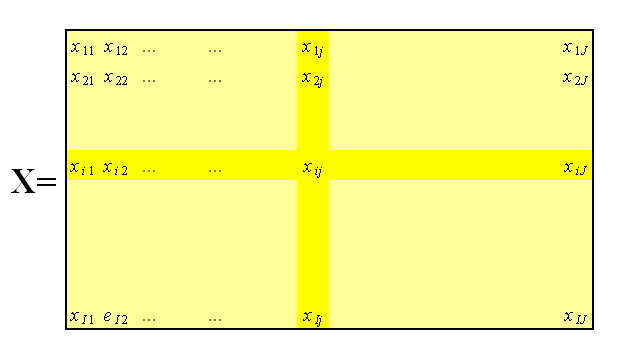
###Базовые сведения Метод главных компонент - способ уменьшить размерность данных с минимальной потерей информации, попутно решающий вопрос классификации исходных объектов. Применяется он к прямоугольной матрице данных X размером IxJ:

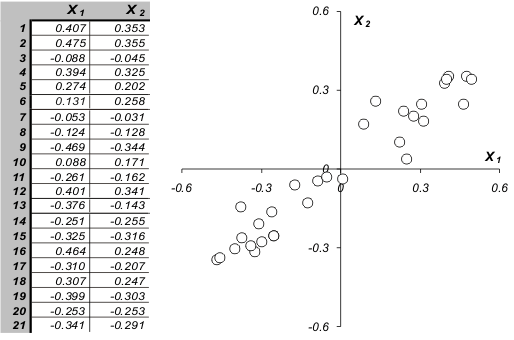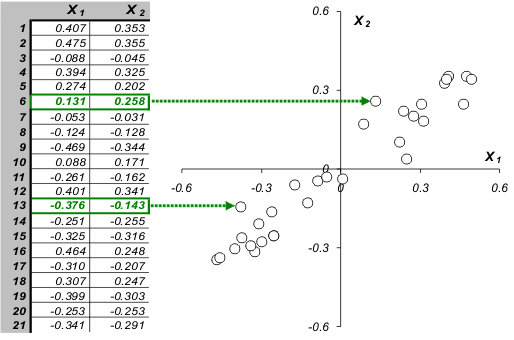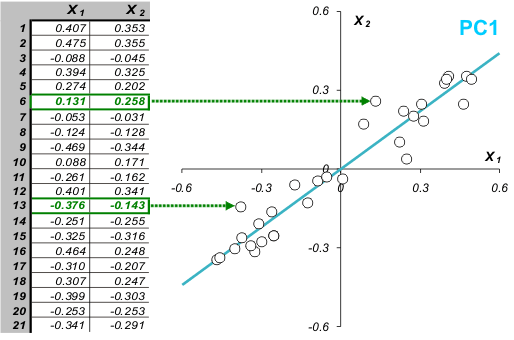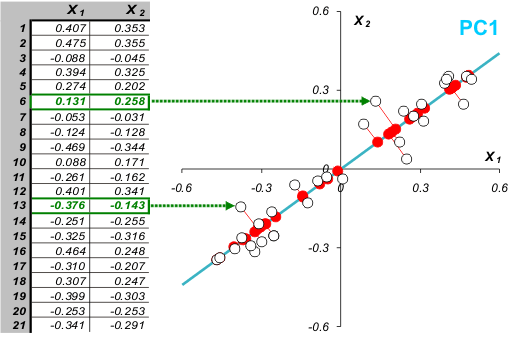
Строки этой матрицы - образцы (индивиды), столбцы - переменные (признаки). Интуитивно в двумерном случае PCA выглядит так:

Каждой строке исходной таблицы (образцу, индивиду) соответствует точка на плоскости с какими-то координатами. Через эти точки проведем прямую вдоль максимального изменения данных. Это и будет так называемая 1-я главная компонента. Спроецируем все точки на эту прямую. Здесь надо сказать, что метод главных компонент оптимален в том смысле, что сумма квадратов отклонений (этих самых проекций) минимальна среди всех других прочих. Эти отклонения могут быть шумом, т.е. случайным набором величин, а могут нести в себе информацию. В этом случае снова ищем ось максимального изменения данных (перперндикулярно первой) и т.д.

В общем, многомерном случае, процесс выделения главных компонент происходит так:

1. Ищется центр облака данных, и туда переносится новое начало координат – это нулевая главная компонента (PC0)
2. Выбирается направление максимального изменения данных – это первая главная компонента (PC1)
3. Если данные описаны не полностью (шум велик), то выбирается еще одно направление (PC2) – перпендикулярное к первому, так чтобы описать оставшееся изменение в данных и т.д.

В итоге мы переходим от большого количества переменных к представлению их в гораздо меньшей размерности. Более того, мы даже сами можем выбирать, представление какой размерности мы хотим получить (сколько ищем главных компонент - такая и размерность). Найденные главные компоненты и есть скрытые, латентные переменные, управляющие устройством всех данных.

Еще один пример на пальцах. Пусть h - высота, w - ширина например картины. Пусть новая характеристика (главная компонента) имеет вид s = hw. Как видно, это есть площадь. Таким образом, можно интерпретировать s как размер картины, по которому мы можем их упорядочить.

###Формальный алгоритм Пусть имеется матрица переменных X размерностью I×J, где I – число образцов (строк), а J – это число независимых переменных (столбцов), которых, как правило, много. В методе главных компонент ищутся новые переменные(главные компоненты) ta(a = 1...A), являющиеся линейной комбинацией исходных переменных xj (j=1,…J) ta = pa1x1+… + paJxJ

С помощью этих новых переменных матрица X разлагается в произведение двух матриц T и P:

Матрица T называется матрицей счетов (scores). Ее размерность I×A.

Матрица P называется матрицей нагрузок (loadings). Ее размерность J×A.

E – это матрица остатков, размерностью I×J.

Важным свойством PCA является ортогональность (независимость) главных компонент. Поэтому матрица счетов T не перестраивается при увеличении числа компонент, а к ней просто прибавляется еще один столбец – соответствующий новому направлению. Тоже происходит и с матрицей нагрузок P.

Вообще говоря есть два способа реализации метода главных компонент. С точки зрения написания например на Java - проще использовать итерационный (см. 6 стр.) На R можно использовать широчайшую библиотеку методов и функций (в том числе там реализован и сам метод главных компонент, правда он считает только сами главные компоненты, а это не исчерпывающая информация об исходных данных). В этой программной среде гораздо более удобно использовать так называемое SVD-разложение исходной матрицы X (Singular Value Decomposition): матрица X разлагается в произведение трех матриц:

(за подробностями сюда)

Тогда T=US, P=V

###Матрица счетов Матрица счетов T дает нам проекции исходных образцов на подпространство главных компонент. Графики счетов дают наглядное представление устройства данных. Близость двух точек означает их схожесть, т.е. положительную корреляцию. Точки, расположенные под прямым углом, являются некоррелироваными, а расположенные диаметрально противоположно – имеют отрицательную корреляцию. Кроме того, из нее можно извлечь определенные характеристики, показывающие важность каждой главной компоненты, т.е. процент дисперсии, вносимой ей в исходные данные.

###Матрица нагрузок Матрица нагрузок P это матрица перехода из исходного пространства переменных в пространство главных компонент. График нагрузок применяется для исследования роли переменных. На этом графике каждая переменная отображается точкой в координатах пространства главных компонент. Анализируя его аналогично графику счетов, можно понять, какие переменные связаны, а какие независимы. Совместное исследование парных графиков счетов и нагрузок может дать много полезной информации о данных.

###Подготовка данных Во многих случаях, перед применением PCA, исходные данные нужно предварительно подготовить: отцентрировать и/или отнормировать. Эти преобразования проводятся по столбцам – переменным.

Центрирование – это вычитание из каждого столбца среднего (по столбцу) значения. Второе простейшее преобразование данных – это нормирование. Это преобразование выравнивает вклад разных переменных в PCA модель. При этом преобразовании каждый столбец делится на свое стандартное отклонение.

###Выбор числа главных компонент Обычно довольно исчерпывающую информацию дают графики 1-2 и 3-4 главных компонент. Как правило, процент дисперсии вносимой остальными ГК довольно мал. Но это всегда можно проверить.

###Проблема интерпретации Важно четко понимать, как были структурированы исходные данные и что там находилось. Конечно можно применить метод к произвольной прямоугольной матрице из чисел, но в этом случае встает вопрос - как интерпретировать полученные результаты. Стандартно концепция отлично работает на модели "индивид-признак".

###источник