LSTM based AutoEncoder

Keywords: AD, AE, lstm Status: Done Type: paper

Paper Review

paper link : LSTM-based Encoder-Decoder for Multi-sensor Anomaly Detection

모델 설명

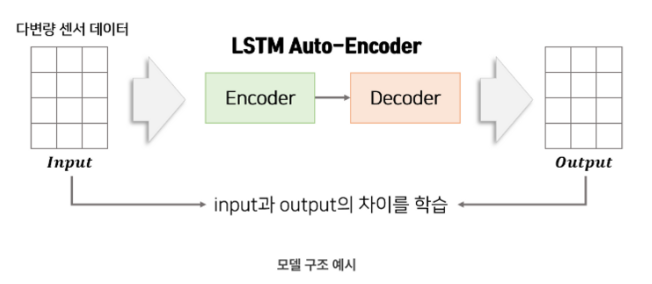
• 정상 데이터를 input으로 입력하여 encoder에서 차원 축소, decoder에서 다시 복원 하는 과정을 거쳐 output이 나온다.
• 인풋과 아웃풋의 차이를 최소화 하도록 학습한다.(MSE 사용)

학습 과정

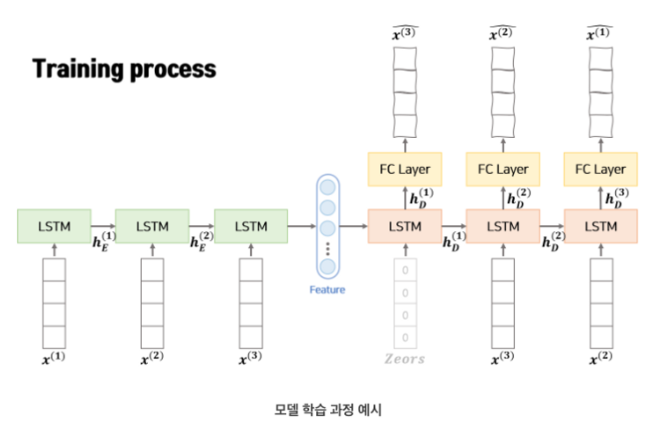
• Teacher Forcing 기법 사용
• initial 값은 0 벡터를 넣음
• X={x(1),x(2),...,x(L)} 형태의 시퀀스가 인풋으로 들어간다. 즉, window size = L로 정해진다.
• 각각의 시점의 x 벡터 역시 x(i)∈Rm 으로 m 차원 벡터로 이루어져 있다.
• encoder에서 학습된 hE(L) 를(한 번에 들어가는 window size가 L 이므로 마지막에 전달되는 hidden layer의 번호는 L 번이다.) Decoder에 전달해준다.
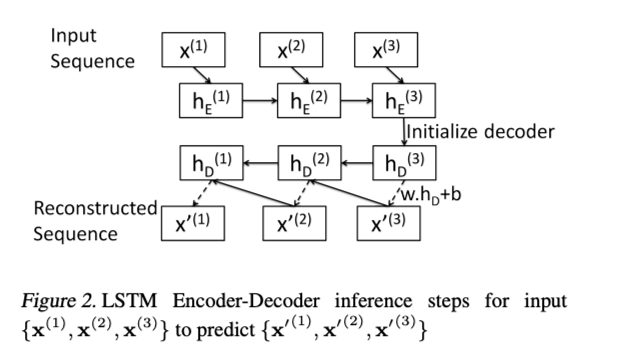
• 아웃풋은 X′={x′(L),x′(L−1),...,x′(1)} 형태의 역순으로 나온다.

X′(i)=wThD(i)+b

• Decoder에서 x′을 예측할때 위와 같은 fc layer를 거친다.

Loss Function

ΣX∈SNΣi=1L∣∣X(i)−X′(i)∣∣2

• S, N은 normal 데이터 셋 (데이터 셋에 대한 설명은 밑에서 보다 자세하게 설명)

추론 과정

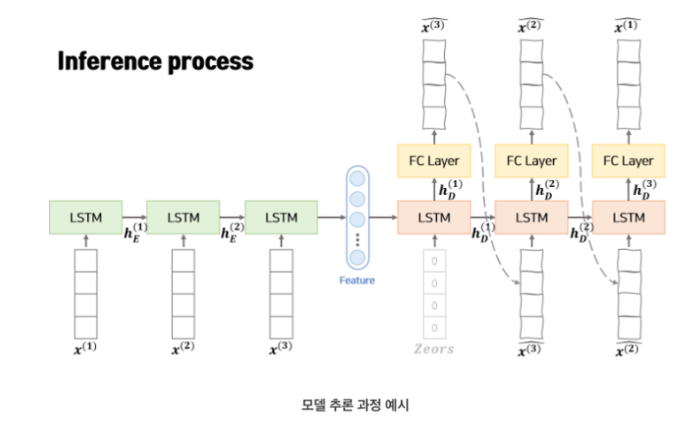
• 추론 과정에서는 teacher forcing 없이 이전 스텝의 데이터를 사용합니다.

Computing likelihood of anomaly

1. Data

   

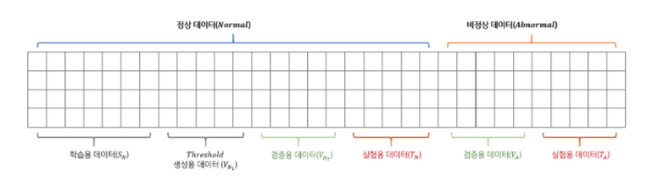
   • sN,vN1,vN2,tN 은 정상 데이터, vA,tA는 비정상 데이터로 분류
   • sN는 학습에 사용
   • vN1는 후술할 τ를 구하기 위한 데이터

2. Reconstruction Error

   e(i)=∣∣x(i)−x′(i)∣∣

   e(i) : i 지점의 Reconstruction Error

   • ti 데이터 셋을 활용해 e를 구한다.

3. Anomaly Score

   a(i)=(e(i)−μ)TΣ−1(e(i)−μ)

4. μ와 Σ 구하기

   • 데이터 셋트 vN1을 사용하여 μ와 Σ 를 구한다.
   • e의 평균을 MLE를 통해서 구하고 구한 평균으로 Σ를 구한다.

5. τ(=threshold) 구하기

   • a(i)>τ 이면 지점 (i)를 이상치라고 정의함.

6. Fβ Score

   Fβ=(1+β2)×P×R/(β2P+R)

   P:Precision

   R:Recall

   • Fβ score는 β>1이면 Precision이, β<1이면 Recall에 더 가중치를 두는 방식이다.

참고 자료

1. LSTM-based Encoder-Decoder for Multi-sensor Anomaly Detection
2. [코드리뷰]LSTM-based Anomaly Detection - 새내기 코드 여행
3. 분류 성능 평가 지표 : F1 Score, F-Beta Score, Macro-F1 정리
4. 분류성능평가지표 - Precision(정밀도), Recall(재현율) and Accuracy(정확도)