In this project, I’ve implemented multiple methods for multiplying matrices, and relevant utilities. My prime focuses were:
-
Cache locality, memory access patterns.
-
SIMD, hand optimized AVX/FMA intrinsics.
-
Software prefetching to maximize pipeline utilization.
-
Cache friendly multithreading.
I didn’t implement the Strassen’s algorithm, this code runs on O(N^3).
Requirements:
- Windows platform
- 64-bit Intel CPU with AVX / FMA support
Currently, if you're looking to use this code, just copy and include CPUUtils.* ThreadPool.h and copy the contents of MatrixMul.cpp except main() into a namespace, the code should be ready to compile as a header only library. Will tidy up the code into a proper library soon.
Note that this program relies on Intel specifix cpuid responses and intrinsics and Win32 API for logical-physical processor mapping and setting thread affinity.
Running the example code:
Build the solution (see build options), then navigate to x64\Release\ and run this command or call “run.bat”. If
you don’t have “tee” command, just delete the last part or install
GnuWin32 CoreUtils.
for /l %x in (1, 1, 100) do echo %x && (MatrixGenerator.exe && printf "Generated valid output. Testing...\n" && MatrixMult.exe matrixA.bin matrixB.bin matrixAB-out.bin && printf \n\n ) | tee -a out.txtOn my machine (6 core i7-8700K), I’ve compared my implementation against:
- Eigen library (with all the compiler optimizations turned on)
- I've tested both Eigen's own implementation and Eigen compiled with MKL+TBB backend, runtime analysis shows that the benchmark indeed uses MKL kernel for matrix multiplication and Eigen doesn't introduce any overheads.
- Multithreaded python-numpy which uses C/C++ backend and Intel MKL BLAS library. The code can be found under the Benchmarks folder, however the graph below doesn't include it as it was consistently slower than Eigen(MKL+TBB)
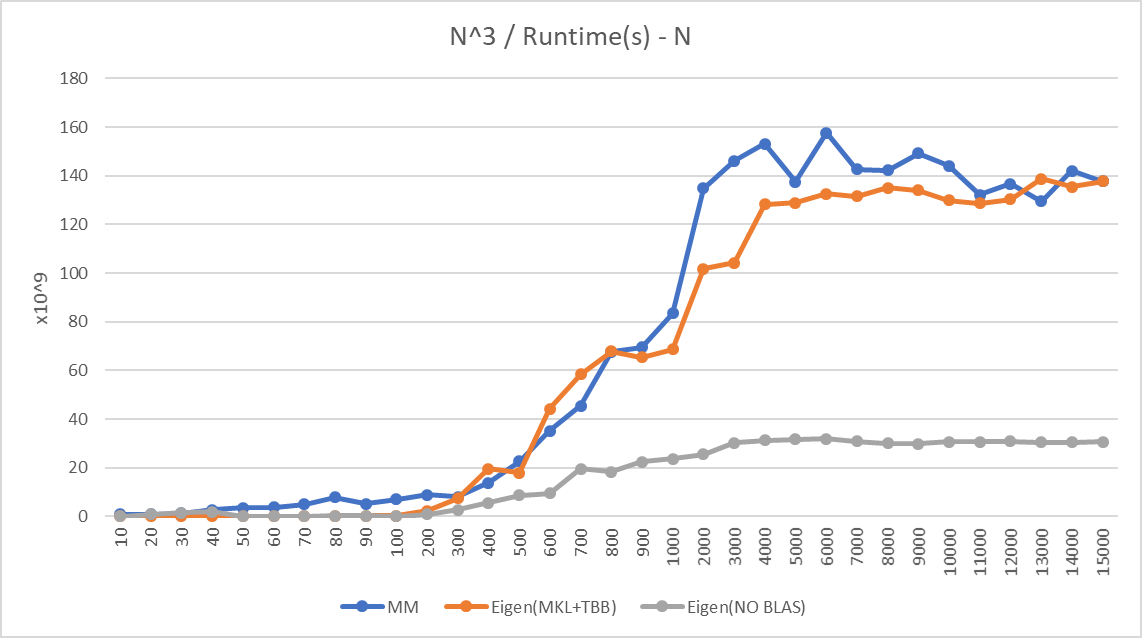
Current implementation runs identically or slightly faster than Eigen (MKL+TBB) for all test cases (tested up to N=15K)! Intel Advisor and VTune clearly shows that MKL kernel avx2_dgemm_kernel_0 is used and no abnormal overheads are present.
Multithreading utilities (ThreadPool.h)
Namespace CPUUtil,
HWLocalThreadPool(NumOfCoresToUse, NumThreadsPerCore) CPUUtil namespace has utility functions for querying runtime system for logical-physical processor mapping, cache sizes, cache line size, hyperthreading, AVX/FMA instruction set support and few more.
I’ve also implemented a hardware local thread pool to handle jobs for multithreaded MTMatMul function. The pool runs every thread corresponding to a job on the same physical core. Idea is that, on hyperthreaded systems such as mine, 2 threads that work on contiguous parts of memory should live on the same core and share the same L1 and L2 cache.
-
Each job is described as an array of N functions. (N=2)
-
For each job, N threads (that were already created) are assigned respective functions.
-
For a given job, all threads are guaranteed to be on the same physical core.
-
No two threads from different jobs are allowed on the same physical core.
-
Maximum optimization: /O2
-
Favor fast code /Ot
-
Enable function level linking: /Gy
-
Enable enhanced instruction set: /arch:AVX2
-
Floating point model: /fp:fast
-
Language: /std:c++17 (for several “if constexpr”s, and one std::lcm. otherwise can be compiled with C++ 11)
Still a factor of 2 to achieve MKL performance.Achieved and surpassed Eigen(MKL+TBB) performance for most test cases N<15K. Test and optimize for larger matrices.- Right now, when the prefetch switches are enabled, instruction retirement rate is about 88%, and the program is neither front-end nor back-end bound, it has excellent pipeline utilization. When the switches are disabled, the retirement rate drops to about 50%, and the program is heavily memory bound, pipelines are heavily stalled due to these bounds. However, on my current system (i7 8700K), binary without prefetching actually computes the output significantly faster (15%). I think this behaviour will heavily rely on the specific CPU, its cache size and performance. Try this on other hardware with different cache performances and varying matrix sizes.
- Wrap the functionality in a replicable and distributable framework that's easy to use.
Note: Debugging builds will have arguments pre-set on the MatrixMul.cpp, you can ignore or revert those to accept argument from command line.
- Cleaned up the code. Split some behaviours into seperate functions.
- Implemented runtime detection for best block size parameters for the runtime system.
- Tuned software prefetching, now we do multiple smaller prefetches in between arithmetic operations and with a stride between prefetches.
- More arithmetically dense inner loop. Instead of 3x3 blocks, do 4x3 blocks (3b + 12c + 1 temporary a == 16 registers used), 7 loads, 12 arithmetic operations.
- HWLocalThreadPool takes number of cores and threads per core as contructor arguments and is not templated anymore. It never should have been.
- Renamed QueryHWCores namespace to CPUUtils and extended it to support querying cache sizes, HTT/AVX/FMA support etc. using __cpuid.
- Implemented one more level of blocking, first block holds data in L3 while the second holds the data in L2. To avoid the "job" overhead in thread pool system and to allow for explicit software prefetching, threads groups handle the highest level of blocks. (If the job was issued on lower level blocks, the threads need explicit syncing so that they only issue prefetch command once per L3 block.)
- Implemented software prefetching. Now while an L3 block is being computed, next one is loaded into the memory in an asynchronous manner. May implement a similar feature for L2 level blocks later on.
- Removed all but one of the MMHelper_MultBlocks implementations.
- Converted AVX multiply and add intrinsics to fused multiply add intrinsics from FMA set.
- Now the MultBlocks use the loaded __m256 vectors as long as possible without unloading and loading a new one. Just like we keep same values in cache and use them as much as possible without unloading, this is the the same idea applied to YMM registers. This increased Arithmetic Intensity (FLOP/L1 Transferred Bytes) metric from 0.25 to 0.67, speeding up the entire matrix multiplication by the same ratio.
- Now fully integrated VTune into my workflow to analyze the application.
Long and detailed work journal, click to expand
- Added a couple of vector sum implementations in benchmark project to compare different intrinsic approaches. The aim is to achieve maximum throughput with ILP minded design. However compiler optimizes away different ways in which I try to maximize the throughput for my own specific CPU architecture.
- In order to address this issue, I wrote another benchmark with inline assembly and compiled it with GCC (as MSVC doesn't support inline assembly in x64 architecture). First of all, I tested GCC's behaviour with intrinsics and found it to be same as MSVC's for our purposes. Having shown that, I've written volatile inline assembly to force compiler to use my implementation. The tests showed that the compiler optimized the intrinsics to almost the same level when the optimizations are enabled. But compiler optimized versions, and my ASM code, is still not fast enough to compete with BLAS packages. So I'm doing something wrong in the first place and writing ASM is not the answer.
- Benchmarked auto vectorization, naive intrinsics and other 2 intrinsic based block multiplication implementations, last 2 methods are about 15% faster than naive intrinsics and auto vectorized code. But arithmetic intensity (FLOPs / memory accesses) is still quite low.
- Started analyzing the bottlenecks further using **Intel's VTune and Advisor**. It now became apparent that while I was getting similar results from different approaches, each had **different bottlenecks** which at first I couldn't see. So with this detailed information I should be able to address those bottlenecks.
- Added another intrinsic based block multiplication method, changed a few implementations to use **FMA** intructions rather than seperate multiply-adds, to achieve higher throughput.
- When profiling my program I noticed that small block sizes that can fit into L2 cache yielded a lot of L3 misses and large blocks that utilized L3 well and cut down the DRAM fetches, ran into L2 misses. So applying the idea that led to blocking to begin with, I will implement **one more level of blocking** to better utilize multiple layers of cache.
- Fixed memory leaks!
(This is the heap profile of the program after running C1 = AB, freeing C1, then running C2=AB and freeing C2. As can be seen here, all the previously leaked mess (packed tasks, function pointers, CoreHandler member arrays etc. ) is now cleaned up nicely. Note: int[] is the static CPU core to logical processor map,)
- Properly called destructors where CoreHandler objects are created using placement new into a malloc'ed buffer.
- Freed BT.mat (transpose of B) in the methods that use it to convert the problem into row-row dot product.
Changed Add function s.t it accepts std::shared_ptr<std::function<void()>[]>, this is only temporary.- Changed the Add() semantics, now Add function accepts a std::vector<std::function<void()>>. Preferred way of using Add() function now is with initializer lists:
tp.Add({
HWLocalThreadPool<>::WrapFunc(MMHelper_MultBlocks,
matData, subX, matA.height - rowC, rowC, colC, matA, matB, matBT) ,
HWLocalThreadPool<>::WrapFunc(MMHelper_MultBlocks,
matData, subX, matA.height - rowC, rowC, colC + subX, matA, matB, matBT)
});
- Added Eigen benchmarks
- Implemented MatMul which should be the general function exposed to outside. It simply selects betwen MTMatMul and ST_TransposedBMatMul depending on the sizes of the matrices. Current impl.:
A.height*A.width*A.width*B.width < K : ST_TransposedBMatMul o.w : MTMatMul