補足：行列の積
本書において、「行列の内積」という表現を使った箇所がありましたが、正しくは「行列の積」になります（8刷以降は修正済み）。
混乱させてしまい、申し訳ありません。
ここでは、「ベクトルの内積」「行列の積」という用語について、またNumPyのdot（np.dot）について補足させてもらいます。
一次元の配列をベクトルと言います。ここに要素数が同じベクトルが2つあるとき、その2つのベクトルの対応する要素をそれぞれ掛け合わせ、それらを全部足し合わせたものを内積と言います。また、内積はドット積と呼ばれることもあります。
「ベクトルの内積」の例は、Pythonで次のように書くことができます。
import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
np.dot(a, b)
# 32
2次元の配列は行列と言います。行列の積は、次のように計算します。
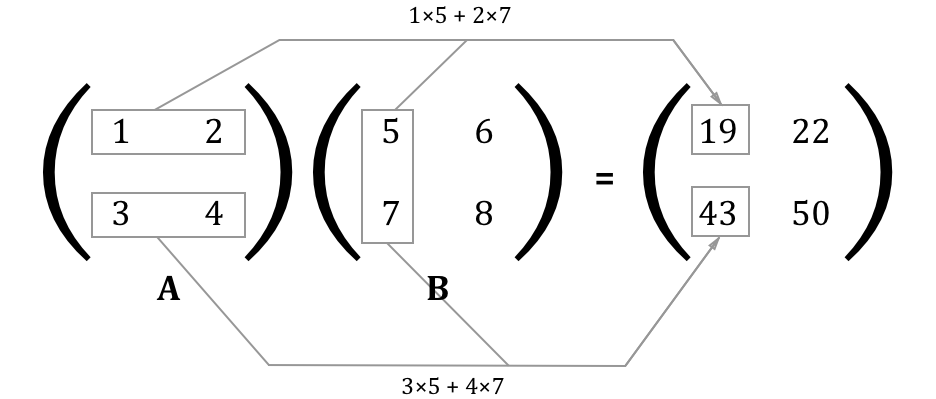
行列の積は、左側の行列の行(横方向)と右側の行列の列 (縦方向)の間の要素ごとの積とその和によって計算が行われます。そして、その計算の結果は新しい多次元配列の要素として格納されます。たとえば、Aの1行目とBの1列目の結果は1行1列目の要素、Aの2行目とBの1列目は2行1列目の要素といったようになります。
np.dotは、1次元配列の場合は「ベクトルの内積」を、2次元配列の場合は「行列の積」を計算します。そのため、Pythonでは次のように書くことができます。
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
np.dot(A, B)
#[[19, 22],
# [43, 50]]
ベクトルについては「内積」または「ドット積」という用語を用います。行列については「行列の積」という表現を用います。NumPyのnp.dotは、1次元配列（ベクトル）の場合は「ベクトルの内積」を、2次元配列（行列）の場合は「行列の積」を計算します。