R-package which allows users to run multi co-moment structural equation models.
Welcome to the new and improved MCMSEM. If you want to use the MCMSEM version as it was used in the original publication, please go to the v0.1.1 release.
This version is considerably more powerful than our previous version. Some highlights:
- Expanded to allow for any N variables instead of just two (use at your own risk)
- Far more flexibility for custom model creation via MCMSEM model objects
- More detailed fit statistics through custom MCMSEM result objects
- Significantly improved performance, and enabled optimization on GPU
- Asymptotic calculation of standard errors (bootstrapping no longer required)
- Exportable data, making it easier for researchers to share moment matrices for MCMSEM without sharing raw data
If you are new to this version of MCMSEM we highly recommend reading our Wiki before starting, as the syntax for using MCMSEM has changed significantly since v0.1.1.
If you use this package please include the following citation:
Tamimy, Z., van Bergen, E., van der Zee, M. D., Dolan, C. V., & Nivard, M. G. (2022, June 30). Multi Co-Moment Structural Equation Models: Discovering Direction of Causality in the Presence of Confounding. https://doi.org/10.31235/osf.io/ynam2
Currently, this package is not listed on CRAN and should therefore be installed from GitHub directly.
library(devtools)
install_github("https://github.com/MichelNivard/MCMSEM")
See the wiki Installing MCMSEM for more details.
See the Installing MCMSEM wiki
Below you will find a short rationale with usage examples of MCMSEM. For more detailed descriptions please visit the wiki.
Let's get going, in this very short pre-tutorial I'll convince you why you should read the entire tutorial, the paper(s) and consider MCMSEM for your projects. This is an advertorial, not a full review of the method with all its good and bad, that's left for the paper and the rest of this wiki.
library(devtools)
install_github("https://github.com/MichelNivard/MCMSEM")
library(MCMSEM)
library(lavaan)
# MAke sure we might be able to replicate this
set.seed(789)
The basic premise is that by modeling higher order co-moments, not just covariance MCMSEM can do incredible things. It can (for example) estimate directional causal effects in the presence of other causal effects in the opposite direction based on continuous variables collected in a cross-sectional and observational setting. Given certain assumptions about the confusers hold even causal effects in the presence of confounding. So to proof that to you, let me simulate data from a dense network with bidirectional causal relations between variables. In the simulation we only use direct paths between variables to induce correlations, no latent variables are present.
b <- matrix(c( 0, .3, 0, .1, .15,
0, 0, 0, .1, .15,
.15, .2, 0, .12, .2,
.15, .15, .1, 0, .3,
.1, .15, .05, 0, 0), 5,5,byrow=T)
# Latent variables don't load on the indicators:
a <- matrix(c(0, 0, 0, 0, 0,
0, 0, 0, 0, 0), ncol=2)
# use the MCMSEM internal simuation tool:
simmdata<- simulate_data(n=100000,a=a,b=b,shape=c(7, 0, 3, 4, 5), df=c(0, 8, 0, 10, 12),asdataframe = T)
#simulate holdout data from the exact same process!
simdata.holdout <- simulate_data(n=50000,a=a,b=b,shape=c(7, 0, 3, 4, 5), df=c(0, 8, 0, 10, 12),asdataframe = T)
cor(simmdata)
[,1] [,2] [,3] [,4] [,5]
[1,] 1.0000000 0.4423112 0.4210967 0.4450527 0.4296345
[2,] 0.4423112 1.0000000 0.4247575 0.4082202 0.3966041
[3,] 0.4210967 0.4247575 1.0000000 0.4683351 0.4801946
[4,] 0.4450527 0.4082202 0.4683351 1.0000000 0.4268477
[5,] 0.4296345 0.3966041 0.4801946 0.4268477 1.0000000
>
So we generated network data, which gives rise to 5 correlated variables, we simulated 25000 observations of 5 variables, we made sure these variables have some skewness and kurtosis.
Then we computed the correlations between the variables, these correlations seem sort of consistent with the influence of a single latent variable (all 5 variables are correlated about equally).
This is a known problem right? the data don't really identify a specific model, and might fit the wrong model rather well, actually. If we fit a latent variable model to these data in lavaan what happens?
### Lavaan naiveness:
# specify a single factor model:
model <- "F1 =~ V1 + V2 + V3 + V4 + V5"
#Fit a single factor modle to the data:
single.factor.model <- sem(model,data = simmdata)
### Based on respectable fit indices, the single factor model has pretty good fit....
fitmeasures(single.factor.model,fit.measures = c("cfi","rmsea"))
cfi rmsea
0.992 0.046
So that's a pretty solid fit to 25000 data points which aren't normally distributed! I think may people would happily accept the (wrong) model fits the data well in this case. Let's look at the estimated parameters, I took liberty of omitting a part of the result (here and in other examples below) to improve readability of the page:
summary(single.factor.model,standardize=T)
lavaan 0.6-12 ended normally after 24 iterations
Estimator ML
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
F1 =~
V1 1.000 0.786 0.656
V2 0.887 0.003 272.326 0.000 0.697 0.626
V3 1.091 0.004 291.463 0.000 0.858 0.689
V4 1.421 0.005 284.822 0.000 1.117 0.666
V5 1.293 0.005 282.941 0.000 1.017 0.659
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.V1 0.820 0.003 309.754 0.000 0.820 0.570
.V2 0.756 0.002 321.343 0.000 0.756 0.608
.V3 0.815 0.003 294.057 0.000 0.815 0.525
.V4 1.569 0.005 305.367 0.000 1.569 0.557
.V5 1.345 0.004 308.145 0.000 1.345 0.565
F1 0.618 0.003 179.721 0.000 1.000 1.000
Okay we can fit the exact same model in MCMSEM, this will take longer, but that's because we are using MCMSEM for a simple model while it's meant for way more complex models...
# Prepare the data:
simmdatasumm <- MCMdatasummary(simmdata)
# specify the MCMSEM single factor model:
mod.single.fac <- MCMmodel(simmdatasumm, n_latent=1,
causal_observed = F ,constrained_a = FALSE)
res.single.fac <- MCMfit(mod.single.fac , simmdatasumm,
optimizers=c("rprop", "lbfgs"), optim_iters=c(5000, 50),
learning_rate=c(0.15,.35), monitor_grads = TRUE,debug = T)
summary(res.single.fac)
|--------------------------------------|
| MCM Result Summary (MCMSEM v0.26.1) |
|--------------------------------------|
device : cpu
N phenotypes : 5
N latents : 1
Parameters summary
label lhs edge rhs est se p last_gradient
1 a1_1 f1 =~ x1 0.6774216 0.002221994 0 -0.00030372804030776
2 a1_2 f1 =~ x2 0.6460607 0.002450077 0 -0.000246435403823853
3 a1_3 f1 =~ x3 0.7112606 0.002113517 0 -0.000320896506309509
4 a1_4 f1 =~ x4 0.6737278 0.002078837 0 -0.000303968787193298
5 a1_5 f1 =~ x5 0.6594946 0.002341010 0 -0.000288307666778564
Variances summary
label lhs edge rhs est se p last_gradient
1 s1 x1 ~~ x1 0.5429684 0.002322939 0 -0.000104825012385845
2 s2 x2 ~~ x2 0.7034848 0.002680491 0 -4.81307506561279e-06
3 s3 x3 ~~ x3 0.4870218 0.002574685 0 -9.28817316889763e-05
4 s4 x4 ~~ x4 0.5476845 0.002248093 0 -0.000122410012409091
5 s5 x5 ~~ x5 0.6263368 0.002268915 0 -4.79742884635925e-05
Skewness summary
label edge v1 v2 v3 est se p last_gradient
1 sk1 ~~~ x1 x1 x1 0.52245688 0.009559851 0.000000e+00 0
2 sk2 ~~~ x2 x2 x2 0.02273338 0.011608215 5.018456e-02 0
3 sk3 ~~~ x3 x3 x3 0.69856018 0.010974598 0.000000e+00 0
4 sk4 ~~~ x4 x4 x4 0.27626094 0.008559417 1.535428e-228 0
5 sk5 ~~~ x5 x5 x5 0.30374101 0.008960798 7.464604e-252 0
Kurtosis summary
label edge v1 v2 v3 v4 est se p last_gradient
1 k1 ~~~~ x1 x1 x1 x1 1.405791 0.02439721 0 -5.7220458984375e-06
2 k2 ~~~~ x2 x2 x2 x2 1.963156 0.03590991 0 4.76837158203125e-06
3 k3 ~~~~ x3 x3 x3 x3 1.769238 0.03414891 0 1.9073486328125e-06
4 k4 ~~~~ x4 x4 x4 x4 1.307484 0.01698693 0 -4.76837158203125e-06
5 k5 ~~~~ x5 x5 x5 x5 1.297236 0.01762279 0 -1.9073486328125e-06
Very similar results if you compare the MCMSEM estimates to the lavaan standardized results (last column in lavaan). This inst too unexpected we fitted very similar models actually (a single factor model).
However, in MCMSEM we can actually use the multivariate skewness and kurtosis between the variables to just estimate the directed network with all paths in all directions! Let's do that now:
mod.network <- MCMmodel(simmdata, n_latent=0,
causal_observed = T,scale_data = T ,constrained_a = FALSE)
res.network <- MCMfit(mod.network , simmdata,
optimizers=c("rprop", "lbfgs"), optim_iters=c(5000, 50),
learning_rate=c(0.15,.35), monitor_grads = TRUE,debug = T)
summary(res.network)
|--------------------------------------|
| MCM Result Summary (MCMSEM v0.26.1) |
|--------------------------------------|
device : cpu
N phenotypes : 5
N latents : 0
Parameters summary
label lhs edge rhs est se p last_gradient
1 b1_2 x1 ~> x2 6.151331e-03 0.006816274 3.668191e-01 0.000175460241734982
2 b1_3 x1 ~> x3 1.452449e-01 0.002979095 0.000000e+00 -4.4724001782015e-05
3 b1_4 x1 ~> x4 1.020069e-01 0.005918295 1.429033e-66 0.000100970733910799
4 b1_5 x1 ~> x5 6.854491e-02 0.005808502 3.866619e-32 0.000267743365839124
5 b2_1 x2 ~> x1 2.755117e-01 0.006062157 0.000000e+00 0.000182127900188789
6 b2_3 x2 ~> x3 1.834408e-01 0.004096662 0.000000e+00 6.35582255199552e-05
7 b2_4 x2 ~> x4 1.017229e-01 0.009157432 1.143939e-28 0.000135798007249832
8 b2_5 x2 ~> x5 1.106104e-01 0.009164575 1.533458e-33 0.000255572609603405
9 b3_1 x3 ~> x1 -9.047752e-05 0.003688662 9.804310e-01 0.000118969241157174
10 b3_2 x3 ~> x2 -3.053474e-03 0.005180531 5.555840e-01 0.000170918647199869
11 b3_4 x3 ~> x4 7.760608e-02 0.004376185 2.302355e-70 0.000154128996655345
12 b3_5 x3 ~> x5 4.493757e-02 0.004955088 1.201422e-19 0.000189122278243303
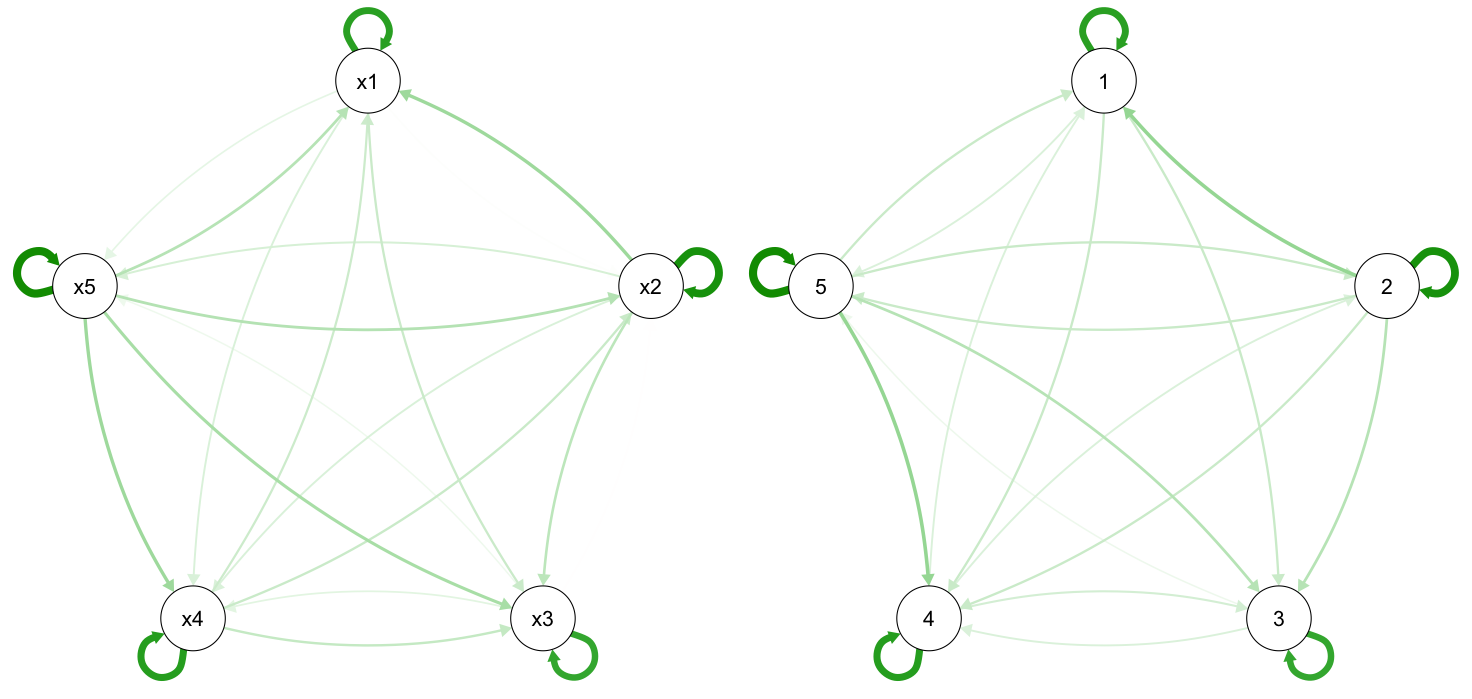
Networks are really better inspected trough visualization then trough staring at path estimates, so lets go ahead and to that:
# and plot:
layout(matrix(c(1,2),1,2))
# Model
plot(res.network,layout="circle")
# Simulated Truth:
b2 <- b + res.network$model$num_matrices$S
qgraph::qgraph(t(b2),layout="circle",diag=T,curveAll=T)
Left we have the estimated network, right the true network, note that in some cases graph changes the arc of the edge but if you look at the direction you'll see these are very similar!
Finally, MCMSEM allows us to compare the two models in terms of fit, and in terms of fit to holdout data we generated previously.
MCMcompareloss(list(res.single.fac,res.network),test_data = simdata.holdout)
mse_train_loss train_chisq train_bic mse_test_loss mse_diff mse_test_chisq mse_test_bic N_parameters
model1 0.4127585292 123827.5588 124079.7895 0.43718457 NA 65577.686 65816.054 20
model2 0.0003538882 106.1665 547.5703 0.01523786 0.4219467 2285.678 2702.822 35
So in the training data (data you used to fit the model) the loss of the network model is way lower than that of the factor model, so are the chi-square statistics, the BIC. In the test data we still have a lower loss for the network model, and a lower chi-square and BIC as well. The network model does have more parameters (complexity): 20 directed edges, 5 skewness parameters, 5 variances, and 5 kurtosis parameters. The added complexity outweighs the cost because the model does (way) better in new data.
This was the advertorial, there are practical theoretical and methodological nuances and limitations, but I bet you are motivated to learn about these now!
For a more detailed description of the various functions used, see our wiki pages.
If you would like to contribute to MCMSEM, please do so via the dev-torch branch.