给你一个有 n 个服务器的计算机网络,服务器编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ,其中 edges[i] = [ui, vi] 表示服务器 ui 和 vi 之间有一条信息线路,在 一秒 内它们之间可以传输 任意 数目的信息。再给你一个长度为 n 且下标从 0 开始的整数数组 patience 。
题目保证所有服务器都是 相通 的,也就是说一个信息从任意服务器出发,都可以通过这些信息线路直接或间接地到达任何其他服务器。
编号为 0 的服务器是 主 服务器,其他服务器为 数据 服务器。每个数据服务器都要向主服务器发送信息,并等待回复。信息在服务器之间按 最优 线路传输,也就是说每个信息都会以 最少时间 到达主服务器。主服务器会处理 所有 新到达的信息并 立即 按照每条信息来时的路线 反方向 发送回复信息。
在 0 秒的开始,所有数据服务器都会发送各自需要处理的信息。从第 1 秒开始,每 一秒最 开始 时,每个数据服务器都会检查它是否收到了主服务器的回复信息(包括新发出信息的回复信息):
- 如果还没收到任何回复信息,那么该服务器会周期性 重发 信息。数据服务器
i每patience[i]秒都会重发一条信息,也就是说,数据服务器i在上一次发送信息给主服务器后的patience[i]秒 后 会重发一条信息给主服务器。 - 否则,该数据服务器 不会重发 信息。
当没有任何信息在线路上传输或者到达某服务器时,该计算机网络变为 空闲 状态。
请返回计算机网络变为 空闲 状态的 最早秒数 。
示例 1:
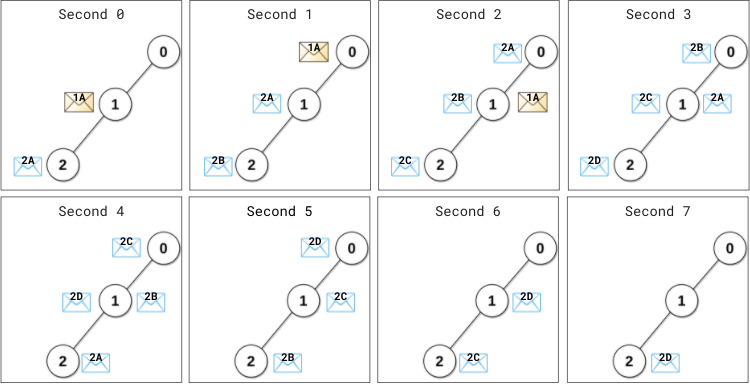
输入:edges = [[0,1],[1,2]], patience = [0,2,1] 输出:8 解释: 0 秒最开始时, - 数据服务器 1 给主服务器发出信息(用 1A 表示)。 - 数据服务器 2 给主服务器发出信息(用 2A 表示)。 1 秒时, - 信息 1A 到达主服务器,主服务器立刻处理信息 1A 并发出 1A 的回复信息。 - 数据服务器 1 还没收到任何回复。距离上次发出信息过去了 1 秒(1 < patience[1] = 2),所以不会重发信息。 - 数据服务器 2 还没收到任何回复。距离上次发出信息过去了 1 秒(1 == patience[2] = 1),所以它重发一条信息(用 2B 表示)。 2 秒时, - 回复信息 1A 到达服务器 1 ,服务器 1 不会再重发信息。 - 信息 2A 到达主服务器,主服务器立刻处理信息 2A 并发出 2A 的回复信息。 - 服务器 2 重发一条信息(用 2C 表示)。 ... 4 秒时, - 回复信息 2A 到达服务器 2 ,服务器 2 不会再重发信息。 ... 7 秒时,回复信息 2D 到达服务器 2 。 从第 8 秒开始,不再有任何信息在服务器之间传输,也不再有信息到达服务器。 所以第 8 秒是网络变空闲的最早时刻。
示例 2:
输入:edges = [[0,1],[0,2],[1,2]], patience = [0,10,10] 输出:3 解释:数据服务器 1 和 2 第 2 秒初收到回复信息。 从第 3 秒开始,网络变空闲。
提示:
n == patience.length2 <= n <= 105patience[0] == 0- 对于
1 <= i < n,满足1 <= patience[i] <= 105 1 <= edges.length <= min(105, n * (n - 1) / 2)edges[i].length == 20 <= ui, vi < nui != vi- 不会有重边。
- 每个服务器都直接或间接与别的服务器相连。
用 BFS 获取主服务器 0 到每个数据服务器的最短距离 step。每个数据服务器 v 从发出信息到收到主服务器的响应信息,所经过的距离(或者时间) d = step * 2,由于数据服务器 v 可能每隔 t = patience[v] 就会重复发送一次消息,可以推算出每个数据服务器 v 最后一次发送消息的时间是 ⌊(d - 1) / t⌋ * t,所以它最后一次收到主服务器的响应信息时间是 ⌊(d - 1) / t⌋ * t + d,空闲时间是 ⌊(d - 1) / t⌋ * t + d + 1,找出所有空间时间的最大值即可。
class Solution:
def networkBecomesIdle(self, edges: List[List[int]], patience: List[int]) -> int:
g = defaultdict(list)
for u, v in edges:
g[u].append(v)
g[v].append(u)
q = deque([0])
vis = {0}
ans = step = 0
while q:
step += 1
for _ in range(len(q)):
u = q.popleft()
for v in g[u]:
if v in vis:
continue
vis.add(v)
q.append(v)
d, t = step * 2, patience[v]
ans = max(ans, (d - 1) // t * t + d + 1)
return ansclass Solution {
public int networkBecomesIdle(int[][] edges, int[] patience) {
int n = patience.length;
List<Integer>[] g = new List[n];
boolean[] vis = new boolean[n];
for (int i = 0; i < n; ++i) {
g[i] = new ArrayList<>();
}
for (int[] e : edges) {
int u = e[0], v = e[1];
g[u].add(v);
g[v].add(u);
}
int ans = 0;
int step = 0;
Deque<Integer> q = new ArrayDeque<>();
q.offer(0);
vis[0] = true;
while (!q.isEmpty()) {
++step;
for (int i = q.size(); i > 0; --i) {
int u = q.poll();
for (int v : g[u]) {
if (vis[v]) {
continue;
}
vis[v] = true;
q.offer(v);
int d = step * 2;
int t = patience[v];
ans = Math.max(ans, (d - 1) / t * t + d + 1);
}
}
}
return ans;
}
}class Solution {
public:
int networkBecomesIdle(vector<vector<int>>& edges, vector<int>& patience) {
int n = patience.size();
vector<vector<int>> g(n);
vector<bool> vis(n);
for (auto& e : edges)
{
int u = e[0], v = e[1];
g[u].push_back(v);
g[v].push_back(u);
}
queue<int> q{{0}};
vis[0] = true;
int ans = 0, step = 0;
while (!q.empty())
{
++step;
for (int i = q.size(); i > 0; --i)
{
int u = q.front();
q.pop();
for (int v : g[u])
{
if (vis[v]) continue;
vis[v] = true;
q.push(v);
int d = step * 2, t = patience[v];
ans = max(ans, (d - 1) / t * t + d + 1);
}
}
}
return ans;
}
};func networkBecomesIdle(edges [][]int, patience []int) int {
n := len(patience)
g := make([][]int, n)
vis := make([]bool, n)
for _, e := range edges {
u, v := e[0], e[1]
g[u] = append(g[u], v)
g[v] = append(g[v], u)
}
q := []int{0}
vis[0] = true
ans, step := 0, 0
for len(q) > 0 {
step++
for i := len(q); i > 0; i-- {
u := q[0]
q = q[1:]
for _, v := range g[u] {
if vis[v] {
continue
}
vis[v] = true
q = append(q, v)
d, t := step*2, patience[v]
ans = max(ans, (d-1)/t*t+d+1)
}
}
}
return ans
}
func max(a, b int) int {
if a > b {
return a
}
return b
}