给你一个points 数组,表示 2D 平面上的一些点,其中 points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 :|xi - xj| + |yi - yj| ,其中 |val| 表示 val 的绝对值。
请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
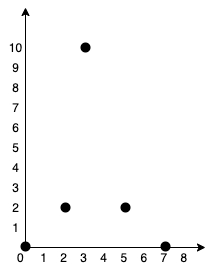
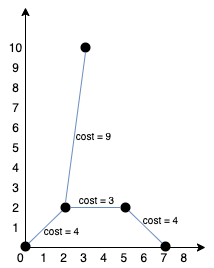
示例 1:
输入:points = [[0,0],[2,2],[3,10],[5,2],[7,0]] 输出:20 解释:我们可以按照上图所示连接所有点得到最小总费用,总费用为 20 。 注意到任意两个点之间只有唯一一条路径互相到达。
示例 2:
输入:points = [[3,12],[-2,5],[-4,1]] 输出:18
示例 3:
输入:points = [[0,0],[1,1],[1,0],[-1,1]] 输出:4
示例 4:
输入:points = [[-1000000,-1000000],[1000000,1000000]] 输出:4000000
示例 5:
输入:points = [[0,0]] 输出:0
提示:
1 <= points.length <= 1000-106 <= xi, yi <= 106- 所有点
(xi, yi)两两不同。
最小生成树问题。
设 n 表示点数,m 表示边数。
方法一:朴素 Prim 算法
时间复杂度 O(n²)。
方法二:Kruskal 算法
先将所有边按照长度由小到大进行排序,循环遍历每条边,逐个加入到图中,当所有点达到一个连通状态时,退出循环,返回此时的总费用即可。
时间复杂度 O(mlogm)。
朴素 Prim 算法:
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
INF = 0x3f3f3f3f
n = len(points)
g = [[0] * n for _ in range(n)]
for i in range(n):
for j in range(n):
if i != j:
x1, y1 = points[i]
x2, y2 = points[j]
g[i][j] = abs(x1 - x2) + abs(y1 - y2)
dist = [INF] * n
vis = [False] * n
ans = 0
for i in range(n):
t = -1
for j in range(n):
if not vis[j] and (t == -1 or dist[t] > dist[j]):
t = j
if i:
ans += dist[t]
for j in range(n):
dist[j] = min(dist[j], g[t][j])
vis[t] = True
return ansKruskal 算法:
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
def find(x):
if p[x] != x:
p[x] = find(p[x])
return p[x]
g = []
n = len(points)
for i, (x1, y1) in enumerate(points):
for j in range(i + 1, n):
x2, y2 = points[j]
g.append((abs(x1 - x2) + abs(y1 - y2), i, j))
g.sort()
p = list(range(n))
ans = 0
for cost, i, j in g:
if find(i) == find(j):
continue
p[find(i)] = find(j)
n -= 1
ans += cost
if n == 1:
return ans
return 0朴素 Prim 算法:
class Solution {
private static final int INF = 0x3f3f3f3f;
public int minCostConnectPoints(int[][] points) {
int n = points.length;
int[][] g = new int[n][n];
int[] dist = new int[n];
boolean[] vis = new boolean[n];
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (i != j) {
int x1 = points[i][0], y1 = points[i][1];
int x2 = points[j][0], y2 = points[j][1];
g[i][j] = Math.abs(x1 - x2) + Math.abs(y1 - y2);
}
}
}
Arrays.fill(dist, INF);
int ans = 0;
for (int i = 0; i < n; ++i) {
int t = -1;
for (int j = 0; j < n; ++j) {
if (!vis[j] && (t == -1 || dist[t] > dist[j])) {
t = j;
}
}
if (i > 0) {
ans += dist[t];
}
for (int j = 0; j < n; ++j) {
dist[j] = Math.min(dist[j], g[t][j]);
}
vis[t] = true;
}
return ans;
}
}Kruskal 算法:
class Solution {
private int[] p;
public int minCostConnectPoints(int[][] points) {
int n = points.length;
List<int[]> g = new ArrayList<>();
for (int i = 0; i < n; ++i) {
int x1 = points[i][0], y1 = points[i][1];
for (int j = i + 1; j < n; ++j) {
int x2 = points[j][0], y2 = points[j][1];
g.add(new int[]{Math.abs(x1 - x2) + Math.abs(y1 - y2), i, j});
}
}
g.sort(Comparator.comparingInt(a -> a[0]));
p = new int[n];
for (int i = 0; i < n; ++i) {
p[i] = i;
}
int ans = 0;
for (int[] e : g) {
int cost = e[0], i = e[1], j = e[2];
if (find(i) == find(j)) {
continue;
}
p[find(i)] = find(j);
ans += cost;
if (--n == 1) {
return ans;
}
}
return 0;
}
private int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
}朴素 Prim 算法:
class Solution {
public:
const int inf = 0x3f3f3f3f;
int minCostConnectPoints(vector<vector<int>>& points) {
int n = points.size();
vector<vector<int>> g(n, vector<int>(n));
vector<int> dist(n, inf);
vector<bool> vis(n);
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < n; ++j)
{
if (i != j)
{
int x1 = points[i][0], y1 = points[i][1];
int x2 = points[j][0], y2 = points[j][1];
g[i][j] = abs(x1 - x2) + abs(y1 - y2);
}
}
}
int ans = 0;
for (int i = 0; i < n; ++i)
{
int t = -1;
for (int j = 0; j < n; ++j)
{
if (!vis[j] && (t == -1 || dist[t] > dist[j]))
{
t = j;
}
}
if (i) ans += dist[t];
for (int j = 0; j < n; ++j) dist[j] = min(dist[j], g[t][j]);
vis[t] = true;
}
return ans;
}
};Kruskal 算法:
class Solution {
public:
vector<int> p;
int minCostConnectPoints(vector<vector<int>>& points) {
int n = points.size();
vector<vector<int>> g;
for (int i = 0; i < n; ++i)
{
int x1 = points[i][0], y1 = points[i][1];
for (int j = i + 1; j < n; ++j)
{
int x2 = points[j][0], y2 = points[j][1];
g.push_back({abs(x1 - x2) + abs(y1 - y2), i, j});
}
}
sort(g.begin(), g.end());
p.resize(n);
for (int i = 0; i < n; ++i) p[i] = i;
int ans = 0;
for (auto& e : g)
{
int cost = e[0], i = e[1], j = e[2];
if (find(i) == find(j)) continue;
p[find(i)] = find(j);
ans += cost;
if (--n == 1) return ans;
}
return 0;
}
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
};朴素 Prim 算法:
func minCostConnectPoints(points [][]int) int {
n := len(points)
inf := 0x3f3f3f3f
g := make([][]int, n)
dist := make([]int, n)
vis := make([]bool, n)
for i, p1 := range points {
dist[i] = inf
g[i] = make([]int, n)
for j, p2 := range points {
if i != j {
x1, y1 := p1[0], p1[1]
x2, y2 := p2[0], p2[1]
g[i][j] = abs(x1-x2) + abs(y1-y2)
}
}
}
ans := 0
for i := 0; i < n; i++ {
t := -1
for j := 0; j < n; j++ {
if !vis[j] && (t == -1 || dist[t] > dist[j]) {
t = j
}
}
if i > 0 {
ans += dist[t]
}
for j := 0; j < n; j++ {
dist[j] = min(dist[j], g[t][j])
}
vis[t] = true
}
return ans
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}Kruskal 算法:
func minCostConnectPoints(points [][]int) int {
n := len(points)
var g [][]int
for i, p := range points {
x1, y1 := p[0], p[1]
for j := i + 1; j < n; j++ {
x2, y2 := points[j][0], points[j][1]
g = append(g, []int{abs(x1-x2) + abs(y1-y2), i, j})
}
}
sort.Slice(g, func(i, j int) bool {
return g[i][0] < g[j][0]
})
ans := 0
p := make([]int, n)
for i := range p {
p[i] = i
}
var find func(x int) int
find = func(x int) int {
if p[x] != x {
p[x] = find(p[x])
}
return p[x]
}
for _, e := range g {
cost, i, j := e[0], e[1], e[2]
if find(i) == find(j) {
continue
}
p[find(i)] = find(j)
ans += cost
n--
if n == 1 {
return ans
}
}
return 0
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}