README.md

1361. 验证二叉树

English Version

题目描述

二叉树上有 n 个节点，按从 0 到 n - 1 编号，其中节点 i 的两个子节点分别是 leftChild[i] 和 rightChild[i]。

只有 所有 节点能够形成且 只 形成 一颗 有效的二叉树时，返回 true；否则返回 false。

如果节点 i 没有左子节点，那么 leftChild[i] 就等于 -1。右子节点也符合该规则。

注意：节点没有值，本问题中仅仅使用节点编号。

 

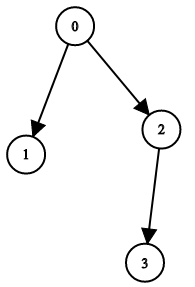
示例 1：

输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
输出：true

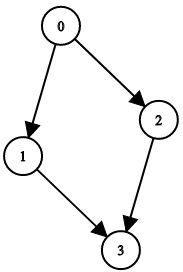
示例 2：

输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
输出：false

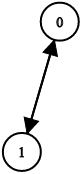
示例 3：

输入：n = 2, leftChild = [1,0], rightChild = [-1,-1]
输出：false

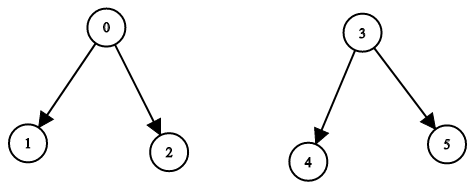
示例 4：

输入：n = 6, leftChild = [1,-1,-1,4,-1,-1], rightChild = [2,-1,-1,5,-1,-1]
输出：false

 

提示：

• 1 <= n <= 10^4
• leftChild.length == rightChild.length == n
• -1 <= leftChild[i], rightChild[i] <= n - 1

解法

并查集。

模板 1——朴素并查集：

# 初始化，p存储每个点的父节点
p = list(range(n))

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]

# 合并a和b所在的两个集合
p[find(a)] = find(b)

模板 2——维护 size 的并查集：

# 初始化，p存储每个点的父节点，size只有当节点是祖宗节点时才有意义，表示祖宗节点所在集合中，点的数量
p = list(range(n))
size = [1] * n

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]

# 合并a和b所在的两个集合
if find(a) != find(b):
    size[find(b)] += size[find(a)]
    p[find(a)] = find(b)

模板 3——维护到祖宗节点距离的并查集：

# 初始化，p存储每个点的父节点，d[x]存储x到p[x]的距离
p = list(range(n))
d = [0] * n

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        t = find(p[x])
        d[x] += d[p[x]]
        p[x] = t
    return p[x]

# 合并a和b所在的两个集合
p[find(a)] = find(b)
d[find(a)] = distance

对于本题，遍历每个节点 i 以及对应的左右孩子 l, r，用 vis 数组记录节点是否有父节点：

• 若孩子节点已存在父节点，说明有多个父亲，不满足条件，直接返回 false。
• 若孩子节点与父节点已经处于同一个连通分量，说明会形成环，不满足条件，直接返回 false。
• 否则，进行合并，并将节点 i 分别与 l, r 进行合并。

遍历结束，判断连通分量个数是否为 1，若是返回 true，否则返回 false。

Python3

class Solution:
    def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:
        p = list(range(n))
        vis = [False] * n

        def find(x):
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        for i in range(n):
            l, r = leftChild[i], rightChild[i]
            if l != -1:
                if vis[l] or find(i) == find(l):
                    return False
                p[find(i)] = find(l)
                vis[l] = True
                n -= 1
            if r != -1:
                if vis[r] or find(i) == find(r):
                    return False
                p[find(i)] = find(r)
                vis[r] = True
                n -= 1
        return n == 1

Java

class Solution {
    private int[] p;

    public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {
        p = new int[n];
        boolean[] vis = new boolean[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        for (int i = 0, t = n; i < t; ++i) {
            int l = leftChild[i], r = rightChild[i];
            if (l != -1) {
                if (vis[l] || find(i) == find(l)) {
                    return false;
                }
                vis[l] = true;
                p[find(i)] = find(l);
                --n;
            }
            if (r != -1) {
                if (vis[r] || find(i) == find(r)) {
                    return false;
                }
                vis[r] = true;
                p[find(i)] = find(r);
                --n;
            }
        }
        return n == 1;
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

C++

class Solution {
public:
    vector<int> p;

    bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {
        p.resize(n);
        for (int i = 0; i < n; ++i) p[i] = i;
        vector<bool> vis(n, false);
        for (int i = 0, t = n; i < t; ++i)
        {
            int l = leftChild[i], r = rightChild[i];
            if (l != -1)
            {
                if (vis[l] || find(i) == find(l)) return false;
                vis[l] = true;
                p[find(i)] = find(l);
                --n;
            }
            if (r != -1)
            {
                if (vis[r] || find(i) == find(r)) return false;
                vis[r] = true;
                p[find(i)] = find(r);
                --n;
            }
        }
        return n == 1;
    }

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
};

Go

var p []int

func validateBinaryTreeNodes(n int, leftChild []int, rightChild []int) bool {
	p = make([]int, n)
	for i := 0; i < n; i++ {
		p[i] = i
	}
	vis := make([]bool, n)
	for i, t := 0, n; i < t; i++ {
		l, r := leftChild[i], rightChild[i]
		if l != -1 {
			if vis[l] || find(i) == find(l) {
				return false
			}
			vis[l] = true
			p[find(i)] = find(l)
			n--
		}
		if r != -1 {
			if vis[r] || find(i) == find(r) {
				return false
			}
			vis[r] = true
			p[find(i)] = find(r)
			n--
		}
	}
	return n == 1
}

func find(x int) int {
	if p[x] != x {
		p[x] = find(p[x])
	}
	return p[x]
}

...