README.md

812. 最大三角形面积

English Version

题目描述

给定包含多个点的集合，从其中取三个点组成三角形，返回能组成的最大三角形的面积。

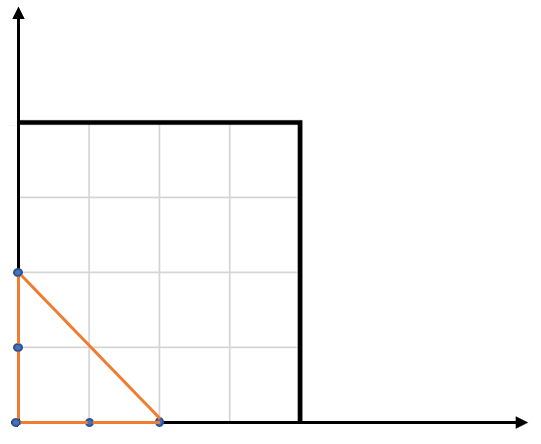
示例:
输入: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
输出: 2
解释: 
这五个点如下图所示。组成的橙色三角形是最大的，面积为2。

注意:

• 3 <= points.length <= 50.
• 不存在重复的点。
•  -50 <= points[i][j] <= 50.
• 结果误差值在 10^-6 以内都认为是正确答案。

解法

Python3

class Solution:
    def largestTriangleArea(self, points: List[List[int]]) -> float:
        ans = 0
        for x1, y1 in points:
            for x2, y2 in points:
                for x3, y3 in points:
                    u1, v1 = x2 - x1, y2 - y1
                    u2, v2 = x3 - x1, y3 - y1
                    t = abs(u1 * v2 - u2 * v1) / 2
                    ans = max(ans, t)
        return ans

Java

class Solution {
    public double largestTriangleArea(int[][] points) {
        double ans = 0;
        for (int[] p1 : points) {
            int x1 = p1[0], y1 = p1[1];
            for (int[] p2 : points) {
                int x2 = p2[0], y2 = p2[1];
                for (int[] p3 : points) {
                    int x3 = p3[0], y3 = p3[1];
                    int u1 = x2 - x1, v1 = y2 - y1;
                    int u2 = x3 - x1, v2 = y3 - y1;
                    double t = Math.abs(u1 * v2 - u2 * v1) / 2.0;
                    ans = Math.max(ans, t);
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    double largestTriangleArea(vector<vector<int>>& points) {
        double ans = 0;
        for (auto& p1 : points)
        {
            int x1 = p1[0], y1 = p1[1];
            for (auto& p2 : points)
            {
                int x2 = p2[0], y2 = p2[1];
                for (auto& p3 : points)
                {
                    int x3 = p3[0], y3 = p3[1];
                    int u1 = x2 - x1, v1 = y2 - y1;
                    int u2 = x3 - x1, v2 = y3 - y1;
                    double t = abs(u1 * v2 - u2 * v1) / 2.0;
                    ans = max(ans, t);
                }
            }
        }
        return ans;
    }
};

Go

func largestTriangleArea(points [][]int) float64 {
	ans := 0.0
	for _, p1 := range points {
		x1, y1 := p1[0], p1[1]
		for _, p2 := range points {
			x2, y2 := p2[0], p2[1]
			for _, p3 := range points {
				x3, y3 := p3[0], p3[1]
				u1, v1 := x2-x1, y2-y1
				u2, v2 := x3-x1, y3-y1
				t := float64(abs(u1*v2-u2*v1)) / 2.0
				ans = math.Max(ans, t)
			}
		}
	}
	return ans
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

...