README.md

261. 以图判树

English Version

题目描述

给定编号从 0 到 n - 1 的 n 个结点。给定一个整数 n 和一个 edges 列表，其中 edges[i] = [ai, bi] 表示图中节点 ai 和 bi 之间存在一条无向边。

如果这些边能够形成一个合法有效的树结构，则返回 true ，否则返回 false 。

 

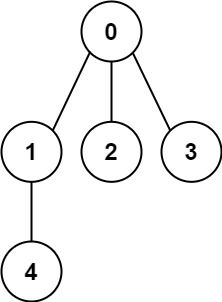
示例 1：

输入: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
输出: true

示例 2:

输入: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
输出: false

 

提示：

• 1 <= n <= 2000
• 0 <= edges.length <= 5000
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• 不存在自循环或重复的边

解法

并查集模板题。

模板 1——朴素并查集：

# 初始化，p存储每个点的父节点
p = list(range(n))

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]

# 合并a和b所在的两个集合
p[find(a)] = find(b)

模板 2——维护 size 的并查集：

# 初始化，p存储每个点的父节点，size只有当节点是祖宗节点时才有意义，表示祖宗节点所在集合中，点的数量
p = list(range(n))
size = [1] * n

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]

# 合并a和b所在的两个集合
if find(a) != find(b):
    size[find(b)] += size[find(a)]
    p[find(a)] = find(b)

模板 3——维护到祖宗节点距离的并查集：

# 初始化，p存储每个点的父节点，d[x]存储x到p[x]的距离
p = list(range(n))
d = [0] * n

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        t = find(p[x])
        d[x] += d[p[x]]
        p[x] = t
    return p[x]

# 合并a和b所在的两个集合
p[find(a)] = find(b)
d[find(a)] = distance

Python3

class Solution:
    def validTree(self, n: int, edges: List[List[int]]) -> bool:
        def find(x):
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        p = list(range(n))
        for a, b in edges:
            if find(a) == find(b):
                return False
            p[find(a)] = find(b)
            n -= 1
        return n == 1

Java

class Solution {
    private int[] p;

    public boolean validTree(int n, int[][] edges) {
        p = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        for (int[] e : edges) {
            int a = e[0], b = e[1];
            if (find(a) == find(b)) {
                return false;
            }
            p[find(a)] = find(b);
            --n;
        }
        return n == 1;
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

C++

class Solution {
public:
    vector<int> p;

    bool validTree(int n, vector<vector<int>>& edges) {
        p.resize(n);
        for (int i = 0; i < n; ++i) p[i] = i;
        for (auto& e : edges)
        {
            int a = e[0], b = e[1];
            if (find(a) == find(b)) return 0;
            p[find(a)] = find(b);
            --n;
        }
        return n == 1;
    }

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
};

Go

func validTree(n int, edges [][]int) bool {
	p := make([]int, n)
	for i := range p {
		p[i] = i
	}
	var find func(x int) int
	find = func(x int) int {
		if p[x] != x {
			p[x] = find(p[x])
		}
		return p[x]
	}
	for _, e := range edges {
		a, b := e[0], e[1]
		if find(a) == find(b) {
			return false
		}
		p[find(a)] = find(b)
		n--
	}
	return n == 1
}

JavaScript

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {boolean}
 */
var validTree = function (n, edges) {
    let p = new Array(n);
    for (let i = 0; i < n; ++i) {
        p[i] = i;
    }
    function find(x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
    for (const [a, b] of edges) {
        if (find(a) == find(b)) {
            return false;
        }
        p[find(a)] = find(b);
        --n;
    }
    return n == 1;
};

...