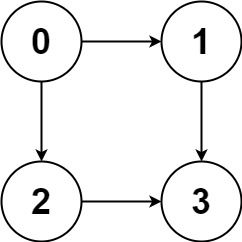
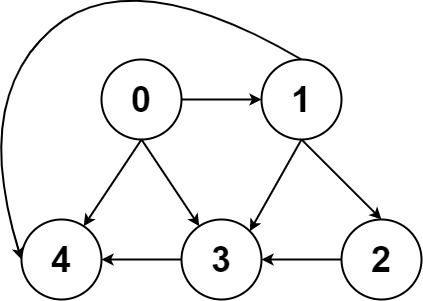
给定一个有 n 个节点的有向无环图,用二维数组 graph 表示,请找到所有从 0 到 n-1 的路径并输出(不要求按顺序)。
graph 的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些结点(译者注:有向图是有方向的,即规定了 a→b 你就不能从 b→a ),若为空,就是没有下一个节点了。
示例 1:
输入:graph = [[1,2],[3],[3],[]] 输出:[[0,1,3],[0,2,3]] 解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
示例 2:
输入:graph = [[4,3,1],[3,2,4],[3],[4],[]] 输出:[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
示例 3:
输入:graph = [[1],[]] 输出:[[0,1]]
示例 4:
输入:graph = [[1,2,3],[2],[3],[]] 输出:[[0,1,2,3],[0,2,3],[0,3]]
示例 5:
输入:graph = [[1,3],[2],[3],[]] 输出:[[0,1,2,3],[0,3]]
提示:
n == graph.length2 <= n <= 150 <= graph[i][j] < ngraph[i][j] != i- 保证输入为有向无环图
(GAD)
注意:本题与主站 797 题相同:https://leetcode.cn/problems/all-paths-from-source-to-target/
DFS。
class Solution:
def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
ans = []
def dfs(i, path):
if i == len(graph) - 1:
ans.append(path.copy())
return
for j in graph[i]:
path.append(j)
dfs(j, path)
path.pop(-1)
dfs(0, [0])
return ansclass Solution {
private List<List<Integer>> ans;
private int[][] graph;
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
ans = new ArrayList<>();
this.graph = graph;
List<Integer> path = new ArrayList<>();
path.add(0);
dfs(0, path);
return ans;
}
private void dfs(int i, List<Integer> path) {
if (i == graph.length - 1) {
ans.add(new ArrayList<>(path));
return;
}
for (int j : graph[i]) {
path.add(j);
dfs(j, path);
path.remove(path.size() - 1);
}
}
}class Solution {
public:
vector<vector<int>> graph;
vector<vector<int>> ans;
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
this->graph = graph;
vector<int> path;
path.push_back(0);
dfs(0, path);
return ans;
}
void dfs(int i, vector<int> path) {
if (i == graph.size() - 1)
{
ans.push_back(path);
return;
}
for (int j : graph[i])
{
path.push_back(j);
dfs(j, path);
path.pop_back();
}
}
};func allPathsSourceTarget(graph [][]int) [][]int {
var path []int
path = append(path, 0)
var ans [][]int
var dfs func(i int)
dfs = func(i int) {
if i == len(graph)-1 {
ans = append(ans, append([]int(nil), path...))
return
}
for _, j := range graph[i] {
path = append(path, j)
dfs(j)
path = path[:len(path)-1]
}
}
dfs(0)
return ans
}