02 Translate Lat Lon to Points.md

OSM to Points

This example is to demonstrate how decimal degree coordinates can be translated to cartesian points

Load Libraries

import rhinoscriptsyntax as rs
import xml.etree.ElementTree as ET
import ghpythonlib.treehelpers as th
import math

Setup Constants

R = 6371000

Parse Lat Lon

lat = []
lon = []
tree = ET.parse(filePath)
root = tree.getroot()
for element in root.findall('node'):
    lat.append(float(element.get('lat')))
    lon.append(float(element.get('lon')))

Parse Bounds

for element in root.findall('bounds'):
    minlat = float(element.get('minlat'))
    minlon = float(element.get('minlon'))
    maxlat = float(element.get('maxlat'))
    maxlon = float(element.get('maxlon'))

Find midpoint (Centre of Bounding Box)

midlat = (minlat+maxlat)/2
midlon = (minlon+maxlon)/2

Calculate distance per degree

Math behind the code

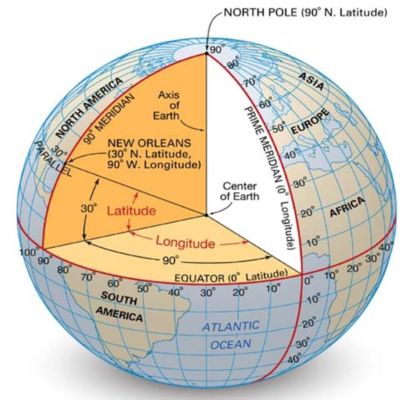
The Longitude distance per degree is along the x-axis remains constant around the circumference of the earth The Latitude distance per degree however, varies. It is largest by the equator and shorter towards the pole since the Latitude lines are parallel to oneanother.

Y Distance

(2 * pi * R) Radian Distance = 360 degrees

Y Distance per degree = (pi * R) / 180 (Where R is the radius of the earth in meters - 6371000m)

X Distance

X Distance per degree = cosine(Latitude) * Y Distance per degree

ydistperdegree = (math.pi*R)/180
xdistperdegree = ((math.cos(midlat*(math.pi/180))*R)*(math.pi/180))

Calculate x and y component of points

x_comp = []
y_comp = []
for i in lon:
    x_comp.append((i-minlon)*xdistperdegree)
for i in lat:
    y_comp.append((i-minlat)*ydistperdegree)
Points = []
for i in range(len(x_comp)):
    Points.append(rs.CreatePoint(x_comp[i],y_comp[i],0))

Create boundary rectangle

plane = rs.WorldXYPlane()
Boundary = rs.AddRectangle(plane,((maxlon-minlon)*xdistperdegree),((maxlat-minlat)*ydistperdegree))