209-长度最小的子数组.md

209-长度最小的子数组

题目信息

题目地址： 209. 长度最小的子数组

题目内容：

给定一个含有n个正整数的数组和一个正整数target。

找出该数组中满足其总和大于等于target的长度最小的连续子数组[numsl, numsl+1, ..., numsr-1, numsr]，并返回其长度。如果不存在符合条件的子数组，返回0。

示例 1：
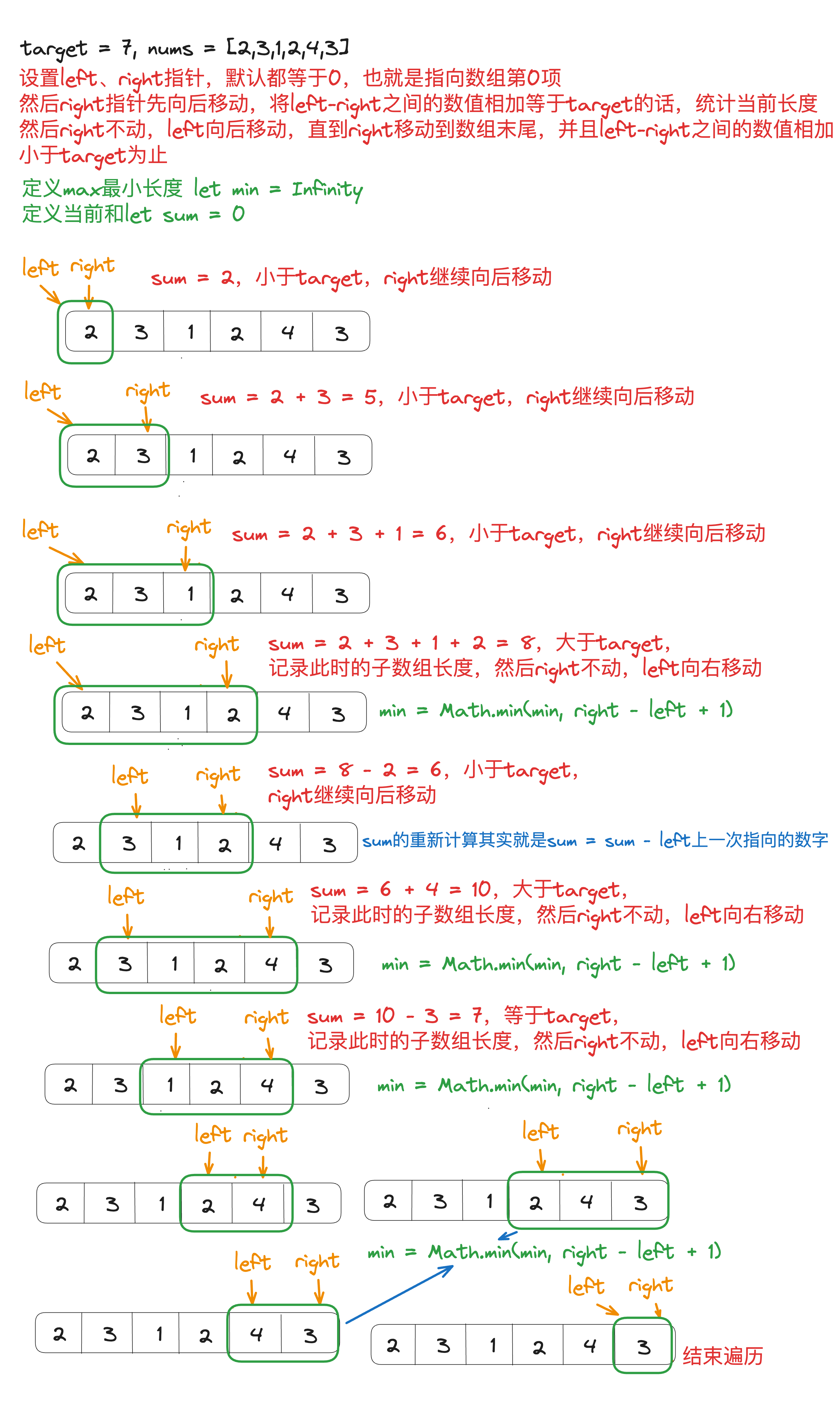
    输入：target = 7, nums = [2,3,1,2,4,3]
    输出：2
    解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：
    输入：target = 4, nums = [1,4,4]
    输出：1

示例 3：
    输入：target = 11, nums = [1,1,1,1,1,1,1,1]
    输出：0

提示：
    1 <= target <= 109
    1 <= nums.length <= 105
    1 <= nums[i] <= 105

进阶：
    如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

题解

解法一

思路：

使用双指针+滑动窗口来实现

1、定义两个指针left和right，初始值都是0，定义一个sum表示子数组中数字的和，minLength表示子数组最小长度，循环数组

2、每次循环将sum加上nums[right]位置的数字

3、如果sum >= target，就计算minLength的值，计算方法就是right - left + 1，因为right和left都是索引所以要+1

然后right指针先别动，将sum减去left位置的数字(sum -= nums[left])，然后重复步骤3，如果步骤3成立，让left指针向后移动一位。再次执行步骤3，直到sum < target为止，然后此时可以继续让right向右移动，直到循环结束

最后返回minLength的值，注意要判断下是否没有符合的子数组，如果没有，minLength就还是初始值，此时要返回0

代码实现：

/**
 * @param {number} target
 * @param {number[]} nums
 * @return {number}
 */
var minSubArrayLen = function(target, nums) {
    let minLength = Infinity;
    let sum = 0;
    let left = 0;
    for(let right = 0; right < nums.length; right++) {
        sum += nums[right];
        // 计算出有符合的选项 记录此时符合的数组长度
        while(sum >= target) {
            minLength = Math.min(minLength, right - left + 1);
            sum -= nums[left++];
        }
    }
    return minLength === Infinity ? 0 : minLength;
};

最外面循环也可以使用while

/**
 * @param {number} target
 * @param {number[]} nums
 * @return {number}
 */
var minSubArrayLen = function(target, nums) {
    let minLength = Infinity
    let sum = 0
    let left = 0
    let right = 0
    while(right < nums.length) {
        sum += nums[right]
        // 计算出有符合的选项 记录此时符合的数组长度
        while(sum >= target) {
            minLength = Math.min(minLength, right - left + 1)
            sum -= nums[left++]
        }
        right++
    }
    return minLength === Infinity ? 0 : minLength
};