ap.md

**1.算法简介**

AP(Affinity Propagation)通常被翻译为近邻传播算法或者亲和力传播算法，是在2007年的Science杂志上提出的一种新的聚类算法。AP算法的基本思想是将全部数据点都当作潜在的聚类中心(称之为exemplar)，然后数据点两两之间连线构成一个网络(相似度矩阵)，再通过网络中各条边的消息(responsibility和availability)传递计算出各样本的聚类中心。


**2.相关概念\(假如有数据点i和数据点j\)**

![](http://images2015.cnblogs.com/blog/1119747/201705/1119747-20170526095101216-1525992044.png)![](http://images2015.cnblogs.com/blog/1119747/201705/1119747-20170526100837825-1748967248.png)![](http://images2015.cnblogs.com/blog/1119747/201705/1119747-20170526100907029-1932825108.png)

 1）相似度： 点j作为点i的聚类中心的能力，记为S\(i,j\)。一般使用负的欧式距离，所以S\(i,j\)越大，表示两个点距离越近，相似度也就越高。使用负的欧式距离，相似度是对称的，如果采用其他算法，相似度可能就不是对称的。

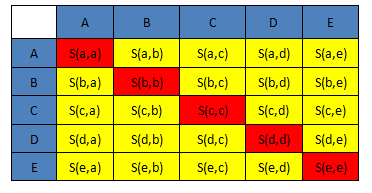
 2）相似度矩阵：N个点之间两两计算相似度，这些相似度就组成了相似度矩阵。如图1所示的黄色区域，就是一个5\*5的相似度矩阵\(N=5\)

 3\)  preference：指点i作为聚类中心的参考度\(不能为0\)，取值为S对角线的值\(图1红色标注部分\)，此值越大，最为聚类中心的可能性就越大。但是对角线的值为0，所以需要重新设置对角线的值，既可以根据实际情况设置不同的值，也可以设置成同一值。一般设置为S相似度值的中值。\(有的说设置成S的最小值产生的聚类最少，但是在下面的算法中设置成中值产生的聚类是最少的\) 

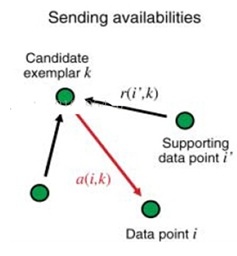
 4）Responsibility\(吸引度\):指点k适合作为数据点i的聚类中心的程度，记为r\(i,k\)。如图2红色箭头所示，表示点i给点k发送信息，是一个点i选点k的过程。

 5）Availability\(归属度\):指点i选择点k作为其聚类中心的适合程度，记为a\(i,k\)。如图3红色箭头所示，表示点k给点i发送信息，是一个点k选diani的过程。

 6）exemplar：指的是聚类中心。

 7）r \(i, k\)加a \(i, k\)越大,则k点作为聚类中心的可能性就越大,并且i点隶属于以k点为聚类中心的聚类的可能性也越大


**3.数学公式**


1）吸引度迭代公式:


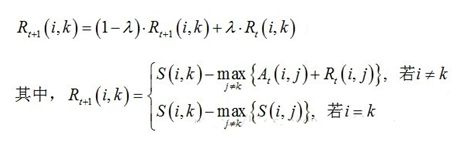![](http://images2015.cnblogs.com/blog/1119747/201705/1119747-20170526101917529-1649493723.png)    （公式一）


说明1：Rt+1\(i,k\)表示新的R\(i,k\)，Rt\(i,k\)表示旧的R\(i,k\)，也许这样说更容易理解。其中λ是阻尼系数，取值\[0.5,1\)，用于算法的收敛
说明2：网上还有另外一种数学公式：


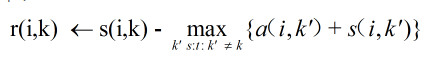![](http://images2015.cnblogs.com/blog/1119747/201705/1119747-20170526102223216-964419606.png)    （公式二）


sklearn官网的公式是：


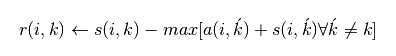![](http://images2015.cnblogs.com/blog/1119747/201705/1119747-20170526103202029-1789533650.png)       （公式三）


我试了这两种公式之后，发现还是公式一的聚类效果最好。同样的数据都采取S的中值作为参考度，我自己写的算法聚类中心是5个，sklearn提供的算法聚类中心是十三个，但是如果把参考度设置为p=-50，则我自己写的算法聚类中心很多，sklearn提供的聚类算法产生标准的3个聚类中心\(因为数据是围绕三个中心点产生的\)，目前还不清楚这个p=-50是怎么得到的。

2）归属度迭代公式


![](http://images2015.cnblogs.com/blog/1119747/201705/1119747-20170526103929544-828180869.png)


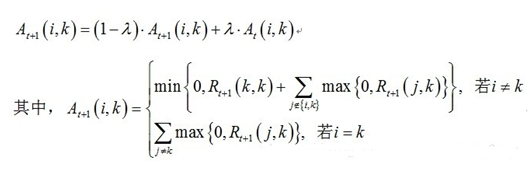
说明：At+1\(i,k\)表示新的A\(i,k\)，At\(i,k\)表示旧的A\(i,k\)。其中λ是阻尼系数，取值\[0.5,1\)，用于算法的收敛


**4.详细的算法流程**

1）设置实验数据。使用sklearn包中提供的函数，随机生成以\[1, 1\], \[-1, -1\], \[1, -1\]三个点为中心的150个数据。

2）计算相似度矩阵，并且设置参考度，这里使用相似度矩阵的中值

3）计算吸引度矩阵，即R值。


 如果有细心的同学会发现，在上述求R和求A的公式中，求R需要A，求A需要R，所以R或者A不是一开始就可以求解出的，需要先初始化，然后再更新。\(我开始就陷入了这个误区，总觉得公式有问题，囧\)


4）计算归属度矩阵，即A值

5）迭代更新R值和A值。终止条件是聚类中心在一定程度上不再更新或者达到最大迭代次数

6）根据求出的聚类中心，对数据进行分类


 这个步骤产生的是一个归类列表，列表中的每个数字对应着样本数据中对应位置的数据的分类