forked from shunliz/Machine-Learning
-
Notifications
You must be signed in to change notification settings - Fork 0
/
cbow-skip-n.md
80 lines (40 loc) · 8.62 KB
/
cbow-skip-n.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
# CBOW与Skip-Gram模型基础
---
word2vec是google在2013年推出的一个NLP工具,它的特点是将所有的词向量化,这样词与词之间就可以定量的去度量他们之间的关系,挖掘词之间的联系。虽然源码是开源的,但是谷歌的代码库国内无法访问,因此本文的讲解word2vec原理以Github上的[word2vec](https://github.com/tmikolov/word2vec)代码为准。本文关注于word2vec的基础知识。
# 1. 词向量基础
用词向量来表示词并不是word2vec的首创,在很久之前就出现了。最早的词向量是很冗长的,它使用是词向量维度大小为整个词汇表的大小,对于每个具体的词汇表中的词,将对应的位置置为1。比如我们有下面的5个词组成的词汇表,词"Queen"的序号为2, 那么它的词向量就是\(0,1,0,0,0\)。同样的道理,词"Woman"的词向量就是\(0,0,0,1,0\)。这种词向量的编码方式我们一般叫做1-of-N representation或者one hot representation.
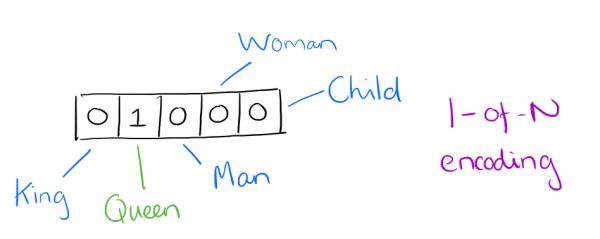
One hot representation用来表示词向量非常简单,但是却有很多问题。最大的问题是我们的词汇表一般都非常大,比如达到百万级别,这样每个词都用百万维的向量来表示简直是内存的灾难。这样的向量其实除了一个位置是1,其余的位置全部都是0,表达的效率不高,能不能把词向量的维度变小呢?
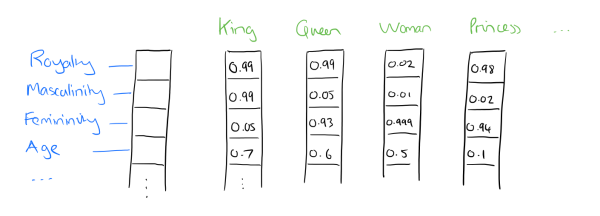
Dristributed representation可以解决One hot representation的问题,它的思路是通过训练,将每个词都映射到一个较短的词向量上来。所有的这些词向量就构成了向量空间,进而可以用普通的统计学的方法来研究词与词之间的关系。这个较短的词向量维度是多大呢?这个一般需要我们在训练时自己来指定。
比如下图我们将词汇表里的词用"Royalty","Masculinity", "Femininity"和"Age"4个维度来表示,King这个词对应的词向量可能是\(0.99, 0.99,0.05, 0.7\)。当然在实际情况中,我们并不能对词向量的每个维度做一个很好的解释。
有了用Dristributed representation表示的较短的词向量,我们就可以较容易的分析词之间的关系了,比如我们将词的维度降维到2维,有一个有趣的研究表明,用下图的词向量表示我们的词时,我们可以发现:$$\vec {King} - \vec {Man} + \vec {Woman} = \vec {Queen}$$
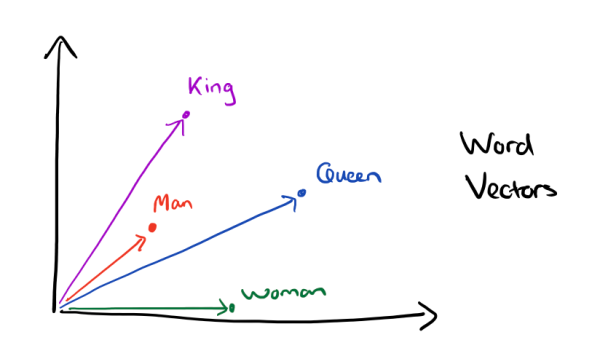
可见我们只要得到了词汇表里所有词对应的词向量,那么我们就可以做很多有趣的事情了。不过,怎么训练得到合适的词向量呢?一个很常见的方法是使用神经网络语言模型。
# 2. CBOW与Skip-Gram用于神经网络语言模型
在word2vec出现之前,已经有用神经网络DNN来用训练词向量进而处理词与词之间的关系了。采用的方法一般是一个三层的神经网络结构(当然也可以多层),分为输入层,隐藏层和输出层\(softmax层\)。
这个模型是如何定义数据的输入和输出呢?一般分为CBOW\(Continuous Bag-of-Words 与Skip-Gram两种模型。
CBOW模型的训练输入是某一个特征词的上下文相关的词对应的词向量,而输出就是这特定的一个词的词向量。比如下面这段话,我们的上下文大小取值为4,特定的这个词是"Learning",也就是我们需要的输出词向量,上下文对应的词有8个,前后各4个,这8个词是我们模型的输入。由于CBOW使用的是词袋模型,因此这8个词都是平等的,也就是不考虑他们和我们关注的词之间的距离大小,只要在我们上下文之内即可。
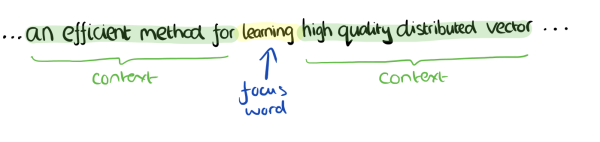
这样我们这个CBOW的例子里,我们的输入是8个词向量,输出是所有词的softmax概率(训练的目标是期望训练样本特定词对应的softmax概率最大),对应的CBOW神经网络模型输入层有8个神经元,输出层有词汇表大小个神经元。隐藏层的神经元个数我们可以自己指定。通过DNN的反向传播算法,我们可以求出DNN模型的参数,同时得到所有的词对应的词向量。这样当我们有新的需求,要求出某8个词对应的最可能的输出中心词时,我们可以通过一次DNN前向传播算法并通过softmax激活函数找到概率最大的词对应的神经元即可。
Skip-Gram模型和CBOW的思路是反着来的,即输入是特定的一个词的词向量,而输出是特定词对应的上下文词向量。还是上面的例子,我们的上下文大小取值为4, 特定的这个词"Learning"是我们的输入,而这8个上下文词是我们的输出。
这样我们这个Skip-Gram的例子里,我们的输入是特定词, 输出是softmax概率排前8的8个词,对应的Skip-Gram神经网络模型输入层有1个神经元,输出层有词汇表大小个神经元。隐藏层的神经元个数我们可以自己指定。通过DNN的反向传播算法,我们可以求出DNN模型的参数,同时得到所有的词对应的词向量。这样当我们有新的需求,要求出某1个词对应的最可能的8个上下文词时,我们可以通过一次DNN前向传播算法得到概率大小排前8的softmax概率对应的神经元所对应的词即可。
以上就是神经网络语言模型中如何用CBOW与Skip-Gram来训练模型与得到词向量的大概过程。但是这和word2vec中用CBOW与Skip-Gram来训练模型与得到词向量的过程有很多的不同。
word2vec为什么 不用现成的DNN模型,要继续优化出新方法呢?最主要的问题是DNN模型的这个处理过程非常耗时。我们的词汇表一般在百万级别以上,这意味着我们DNN的输出层需要进行softmax计算各个词的输出概率的的计算量很大。有没有简化一点点的方法呢?
# 3. word2vec基础之霍夫曼树
word2vec也使用了CBOW与Skip-Gram来训练模型与得到词向量,但是并没有使用传统的DNN模型。最先优化使用的数据结构是用霍夫曼树来代替隐藏层和输出层的神经元,霍夫曼树的叶子节点起到输出层神经元的作用,叶子节点的个数即为词汇表的小大。 而内部节点则起到隐藏层神经元的作用。
具体如何用霍夫曼树来进行CBOW和Skip-Gram的训练我们在下一节讲,这里我们先复习下霍夫曼树。
霍夫曼树的建立其实并不难,过程如下:
输入:权值为$$(w_1,w_2,...w_n)$$的n个节点
输出:对应的霍夫曼树
1)将$$(w_1,w_2,...w_n)$$看做是有n棵树的森林,每个树仅有一个节点。
2)在森林中选择根节点权值最小的两棵树进行合并,得到一个新的树,这两颗树分布作为新树的左右子树。新树的根节点权重为左右子树的根节点权重之和。
3) 将之前的根节点权值最小的两棵树从森林删除,并把新树加入森林。
4)重复步骤2)和3)直到森林里只有一棵树为止。
下面我们用一个具体的例子来说明霍夫曼树建立的过程,我们有\(a,b,c,d,e,f\)共6个节点,节点的权值分布是\(16,4,8,6,20,3\)。
首先是最小的b和f合并,得到的新树根节点权重是7.此时森林里5棵树,根节点权重分别是16,8,6,20,7。此时根节点权重最小的6,7合并,得到新子树,依次类推,最终得到下面的霍夫曼树。
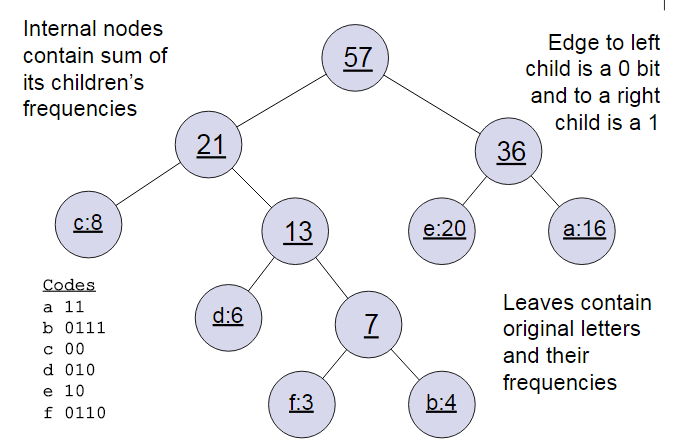
那么霍夫曼树有什么好处呢?一般得到霍夫曼树后我们会对叶子节点进行霍夫曼编码,由于权重高的叶子节点越靠近根节点,而权重低的叶子节点会远离根节点,这样我们的高权重节点编码值较短,而低权重值编码值较长。这保证的树的带权路径最短,也符合我们的信息论,即我们希望越常用的词拥有更短的编码。如何编码呢?一般对于一个霍夫曼树的节点(根节点除外),可以约定左子树编码为0,右子树编码为1.如上图,则可以得到c的编码是00。
在word2vec中,约定编码方式和上面的例子相反,即约定左子树编码为1,右子树编码为0,同时约定左子树的权重不小于右子树的权重。
[https://www.leiphone.com/news/201706/PamWKpfRFEI42McI.html](https://www.leiphone.com/news/201706/PamWKpfRFEI42McI.html)
[https://www.leiphone.com/news/201706/QprrvzsrZCl4S2lw.html](https://www.leiphone.com/news/201706/QprrvzsrZCl4S2lw.html)