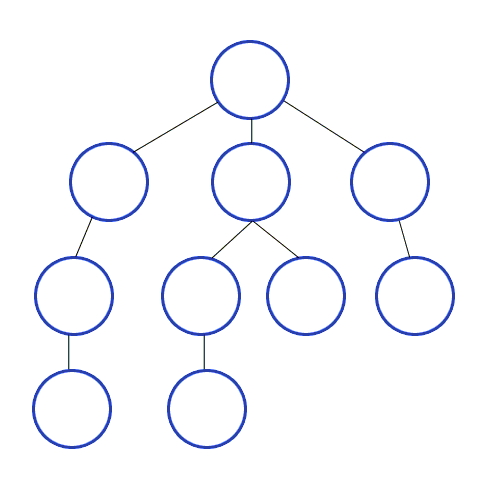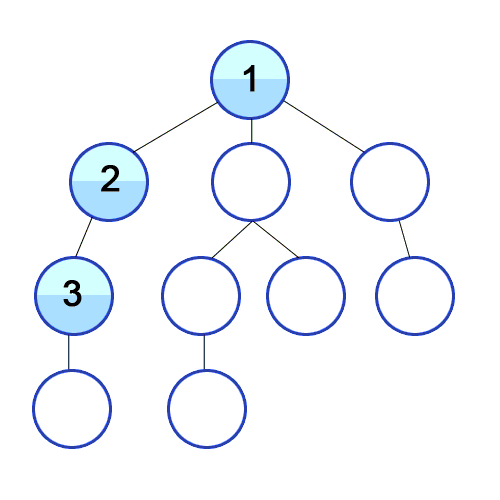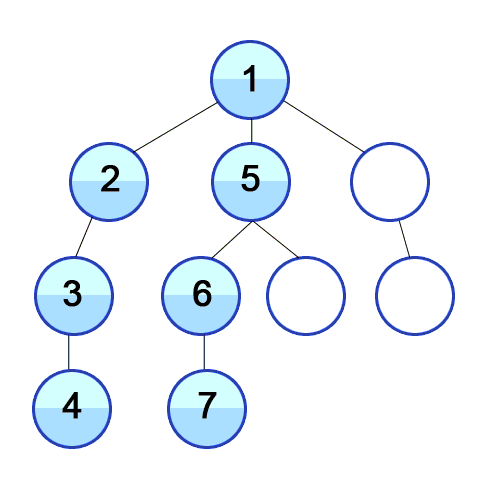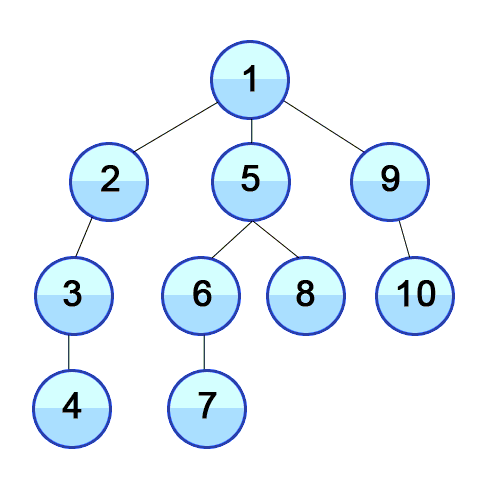
Binary tree as a basic data structure and traversal as a fundamental algorithm, their combination leads to a lot of classic problems. This patern is often seen in many problems, either directly or indirectly.
If you have grasped the traversal of binary trees, other complicated trees will probably be easy for you.
Following are the generally used ways for traversing trees.
-
Depth First Traversals (DFS): Inorder, Preorder, Postorder
-
Breadth First or Level Order Traversal (BFS)
There are applications for both DFS and BFS. Check out leetcode problem No.301 and No.609.
Stack can be used to simplify the process of DFS traversal. Besides, since tree is a recursive data structure, recursion and stack are two key points for DFS.
Graph for DFS:
(from https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/tree/depth-first-search)
The key point of BFS is how to decide whether the traversal of each level is done. The answer is using a variable as a flag to represent the end of the traversal of current level.
Let's dive into details.
related problem144.binary-tree-preorder-traversal
The traversal order of preorder traversal is root-left-right.
Algorithm Preorder
-
Visit the root node and push it into a stack.
-
Pop a node from the stack, and push its right and left child node into the stack respectively.
-
Repeat step 2.
Conclusion: This problem involves the clasic recursive data structure (i.e. a binary tree), and the algorithm above demonstrates how a simplified solution can be reached by using a stack.
If you look at the bigger picture, you'll find that the process of traversal is as followed. Visit the left subtrees repectively from top to bottom, and visit the right subtrees repectively from bottom to top. If we are to implement it from this perspective, things will be somewhat different. For the top to bottom part we can simply use recursion, and for the bottom to top part we can turn to stack.
The traversal will look something like this.
This way of problem solving is a bit similar to backtrack, on which I have written a post. You can benefit a lot from it because it can be used to solve all three DFS traversal problems mentioned aboved. If you don't know this yet, make a memo on it.
related problem94.binary-tree-inorder-traversal
The traversal order of inorder traversal is left-root-right.
So the root node is not printed first. Things are getting a bit complicated here.
Algorithm Inorder
-
Visit the root and push it into a stack.
-
If there is a left child node, push it into the stack. Repeat this process until a leaf node reached.
At this point the root node and all the left nodes are in the stack.
- Start popping nodes from the stack. If a node has a right child node, push the child node into the stack. Repeat step 2.
It's worth pointing out that the inorder traversal of a binary search tree (BST) is a sorted array, which is helpful for coming up simplified solutions for some problems. e.g. 230.kth-smallest-element-in-a-bst and 98.validate-binary-search-tree
related problem145.binary-tree-postorder-traversal
The traversal order of postorder traversal is left-right-root.
This one is a bit of a challange. It deserves the hard tag of leetcode.
In this case, the root node is printed not as the first but the last one. A cunning way to do it is to:
Record whether the current node has been visited. If 1) it's a leaf node or 2) both its left and right subtrees have been traversed, then it can be popped from the stack.
As for 1) it's a leaf node, you can easily tell whether a node is a leaf if both its left and right are null.
As for 2) both its left and right subtrees have been traversed, we only need a variable to record whether a node has been visited or not. In the worst case, we need to record the status for every single node and the space complexity is O(n). But if you come to think about it, as we are using a stack and start printing the result from the leaf nodes, it makes sense that we only record the status for the current node popping from the stack, reducing the space complexity to O(1). Please click the link above for more details.
The key point of level order traversal is how do we know whether the traversal of each level is done. The answer is that we use a variable as a flag representing the end of the traversal of the current level.
Algorithm Level Order
-
Visit the root node, put it in a FIFO queue, put in the queue a special flag (we are using
nullhere). -
Dequeue a node.
-
If the node equals
null, it means that all nodes of the current level have been visited. If the queue is empty, we do nothing. Or else we put in anothernull. -
If the node is not
null, meaning the traversal of current level has not finished yet, we enqueue its left subtree and right subtree repectively.
related problem102.binary-tree-level-order-traversal
We know that there is a tri-color marking in garbage collection algorithm, which works as described below.
-
The white color represents "not visited".
-
The gray color represents "not all child nodes visited".
-
The black color represents "all child nodes visited".
Enlightened by tri-color marking, a bi-color marking method can be invented to solve all three traversal problems with one solution.
The core idea is as followed.
-
Use a color to mark whether a node has been visited or not. Nodes yet to be visited are marked as white and visited nodes are marked as gray.
-
If we are visiting a white node, turn it into gray, and push it's right child node, itself, and it's left child node into the stack respectively.
-
If we are visiting a gray node, print it.
Implementing inorder traversal with tri-color marking:
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
WHITE, GRAY = 0, 1
res = []
stack = [(WHITE, root)]
while stack:
color, node = stack.pop()
if node is None: continue
if color == WHITE:
stack.append((WHITE, node.right))
stack.append((GRAY, node))
stack.append((WHITE, node.left))
else:
res.append(node.val)
return resImplementation of preorder and postorder traversal algorithms can be easily done by changing the order of pushing the child nodes into the stack.
We can also use a method called Morris traversal, which involves no recursion or stack, and the time complexity is O(1).
def MorrisTraversal(root):
curr = root
while curr:
# If left child is null, print the
# current node data. And, update
# the current pointer to right child.
if curr.left is None:
print(curr.data, end= " ")
curr = curr.right
else:
# Find the inorder predecessor
prev = curr.left
while prev.right is not None and prev.right is not curr:
prev = prev.right
# If the right child of inorder
# predecessor already points to
# the current node, update the
# current with it's right child
if prev.right is curr:
prev.right = None
curr = curr.right
# else If right child doesn't point
# to the current node, then print this
# node's data and update the right child
# pointer with the current node and update
# the current with it's left child
else:
print (curr.data, end=" ")
prev.right = curr
curr = curr.leftReference: what-is-morris-traversal