This is an implementation of a sigmoid gated convolutional network, as per https://arxiv.org/pdf/1612.08083v1.pdf.
Run the training process on the GPU:
unset CUDA_VISIBLE_DEVICES
python model.py --train True
Simultaneously run the validation process on the CPU:
export CUDA_VISIBLE_DEVICES=""
python model.py --valid True
The validation process continually loads the latest training weights as both processes run.
The technique described in this paper is an attempt to set up a convolutional network to achieve the same sorts of contextual inputs that an LSTM or RNN is traditionally good at, while taking advantage of the CNNs non-temporal nature to effect big speed gains.
For the language modeling task, this means that the inputs are a sequence of learned word embeddings, and the outputs are that same sequence, but shifted to the left. The final output embedding for a word (a vector within the final hidden layer) is thus trying to predict the word in front of it, a probability which is calculated with the softmax for each vector in the final hidden layer.
In this way, all output projections are computed simultaneously through the convolutional layers. Care must be taken to properly pad the inputs such that each convolution kernel cannot see any context in front of it, as this would constitute data leakage.
We can see that "context" for each word in this scenario is determined by the receptive field of the last layer, which is depends on the kernel widths throughout the entire network, and is thus finite, as opposed to recurrent architectures, which theoretically can have infinite contexts. However, the receptive field can be expressed as a function of the exponent of the layers. As illustrated above, a net with three hidden layers and a kernel size of 3 has, for each token, a receptive field of 9. In this way it is quite easy to achieve very large contexts without requiring the networks to be very deep. The authors also note that in practice, performance tends to decrease for both GCNNs and RNNs as context size increases above 20-25 steps.
As with most language modeling tasks, the most expensive part of the computation is the softmax stage, where each output vector must calculate the probability with respect to the target word. This is expensive because all of the output probabilities must sum to one, so the total across all possible tokens in the vocabulary must be computed as the divisor for normalization.
The authors use a newer technique called the adaptive softmax to approximate the softmax for speed. In this implementation, I use a full softmax, as the vocabulary for Wikitext-2 is not prohibitively large at ~33k. Of course, this will slow things down very much if we tried to train on a bigger dataset like Wikitext-103. However, until I have time to read the adaptive softmax paper [0] and understand how it works, the full softmax suffices.
In this implementation, I use a depthwise 2d convolution, treating each input embedding dimension as a different channel. This particular net is 11 layers deep, with 2 residual layers, and an output embedding projection of 256 dimensions. The kernel width is set to 3 throughout the network, and the sequence length is set at 25. I use weight normalization [1], as per the paper. The batch size is set to 500.
Note: In the original paper, the initial sequence padding is listed to be k/2 (k= kernel width). It should in fact be k-1, as k/2 would allow future context to leak into the current word. I have verified this with the authors and the error will be corrected in the next version of the paper.
Moving forward, there are some likely some interesting experiments to be done around various kernel width/layer depth permutations for identical effective context sizes.
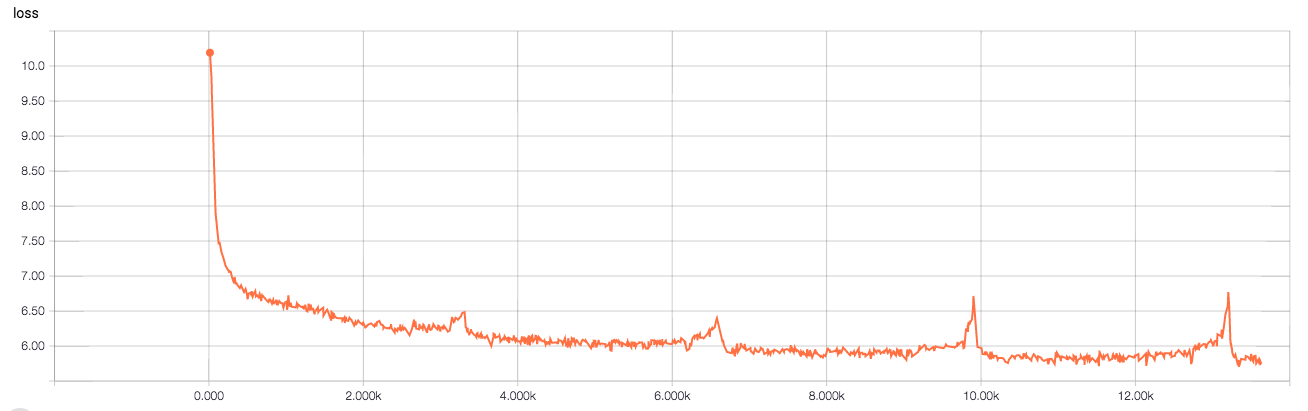
In 14k steps (at a batch size of 500), this is able to achieve a test perplexity of 275 Wikitext-2. SOTA is 68.9 (unknown number of steps)[2]. Below is the validation loss over time:
[0] https://arxiv.org/pdf/1609.04309v2.pdf
