1. 堆结构

「堆排序（Heap sort）」是一种基于「堆结构」实现的高效排序算法。在介绍「堆排序」之前，我们先来了解一下什么是「堆结构」。

1.1 堆的定义

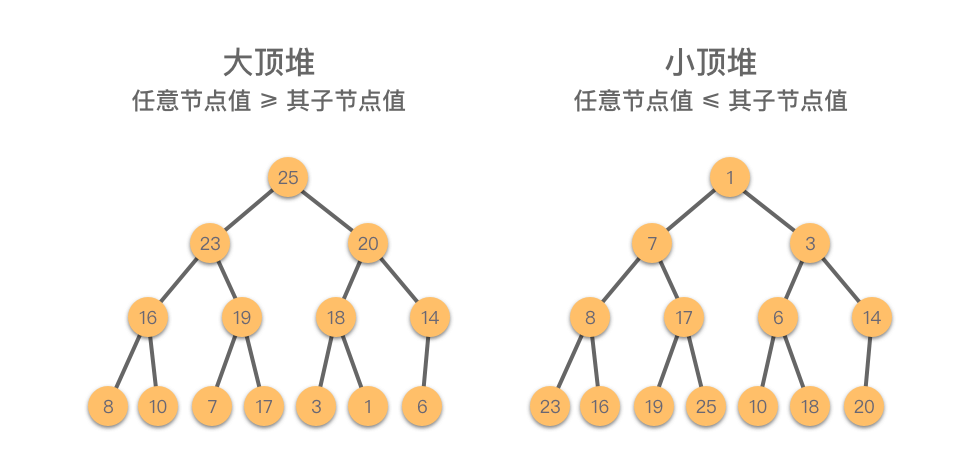
堆（Heap）：一种满足以下两个条件之一的完全二叉树：

大顶堆（Max Heap）：任意节点值 ≥ 其子节点值。

小顶堆（Min Heap）：任意节点值 ≤ 其子节点值。

1.2 堆的存储结构

堆的逻辑结构就是一颗完全二叉树。如下图所示：

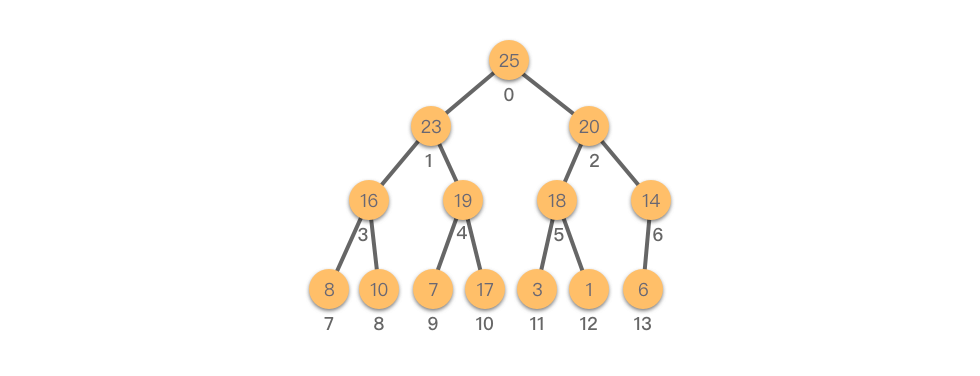
而我们在「07.树 - 01.二叉树 - 01.树与二叉树的基础知识」章节中学过，对于完全二叉树（尤其是满二叉树）来说，采用顺序存储结构（数组）的形式来表示完全二叉树，能够充分利用存储空间。如下图所示：

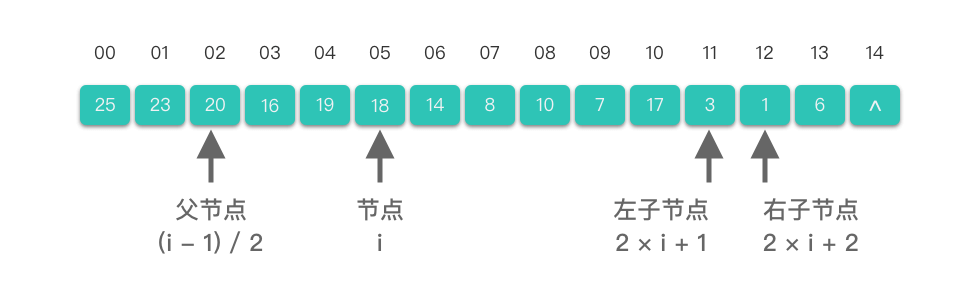
当我们使用顺序存储结构（即数组）来表示堆时，堆中元素的节点编号与数组的索引关系为：

如果某二叉树节点（非叶子节点）的下标为 $i$，那么其左孩子节点下标为 $2 \times i + 1$，右孩子节点下标为 $2 \times i + 2$。
如果某二叉树节点（非根结点）的下标为 $i$，那么其根节点下标为 $\lfloor \frac{i - 1}{2} \rfloor$（向下取整）。

class MaxHeap:
    def __init__(self):
        self.max_heap = []

1.3 访问堆顶元素

访问堆顶元素：指的是从堆结构中获取位于堆顶的元素。

在堆中，堆顶元素位于根节点，当我们使用顺序存储结构（即数组）来表示堆时，堆顶元素就是数组的首个元素。

class MaxHeap:
    ......
    def peek(self) -> int:
        # 大顶堆为空
        if not self.max_heap:
            return None
        # 返回堆顶元素
        return self.max_heap[0]

访问堆顶元素不依赖于数组中元素个数，因此时间复杂度为 $O(1)$。

1.4 向堆中插入元素

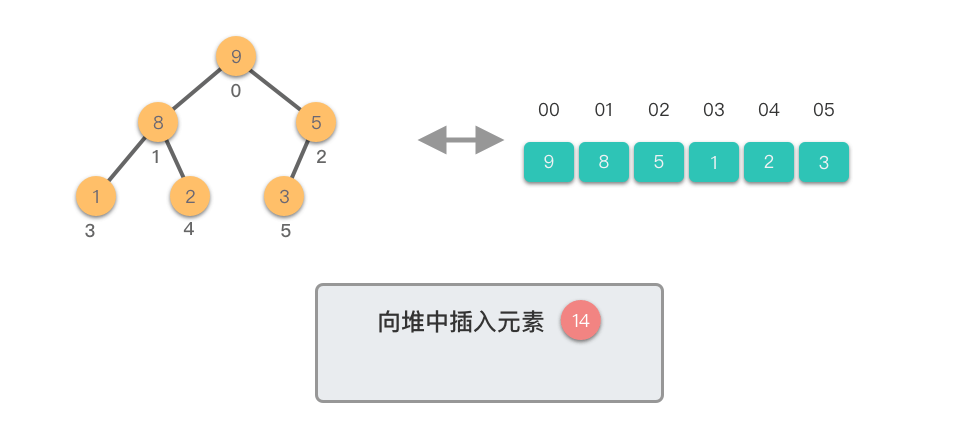
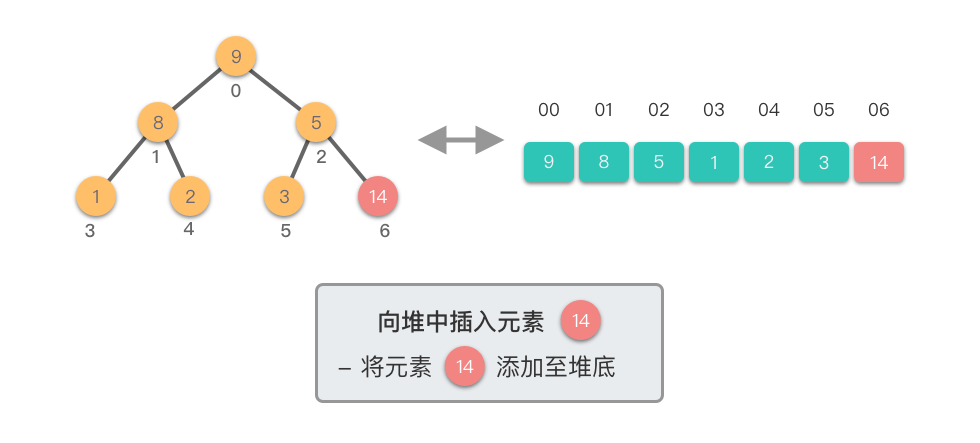
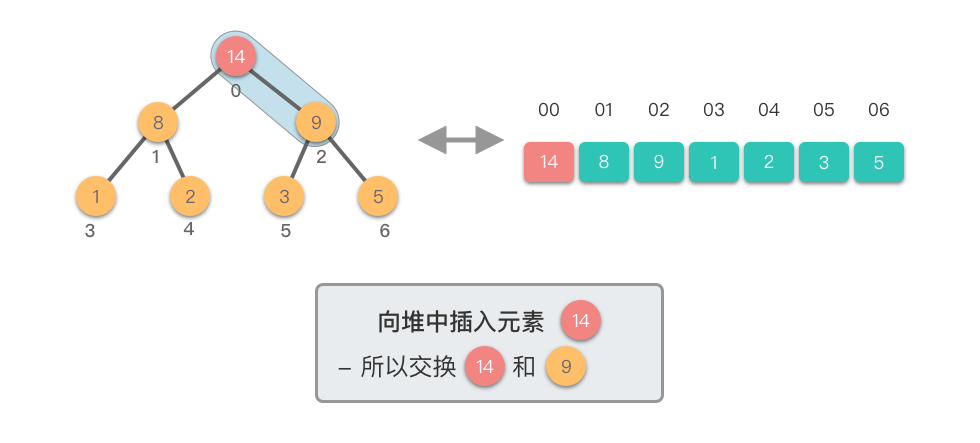
向堆中插入元素：指的将一个新的元素添加到堆中，调整堆结构，以保持堆的特性不变。

向堆中插入元素的步骤如下：

将新元素添加到堆的末尾，保持完全二叉树的结构。
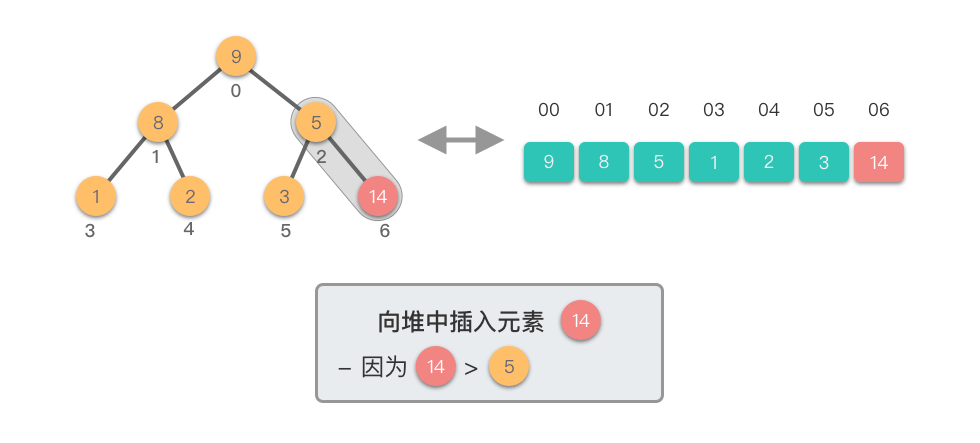
从新插入的元素节点开始，将该节点与其父节点进行比较。
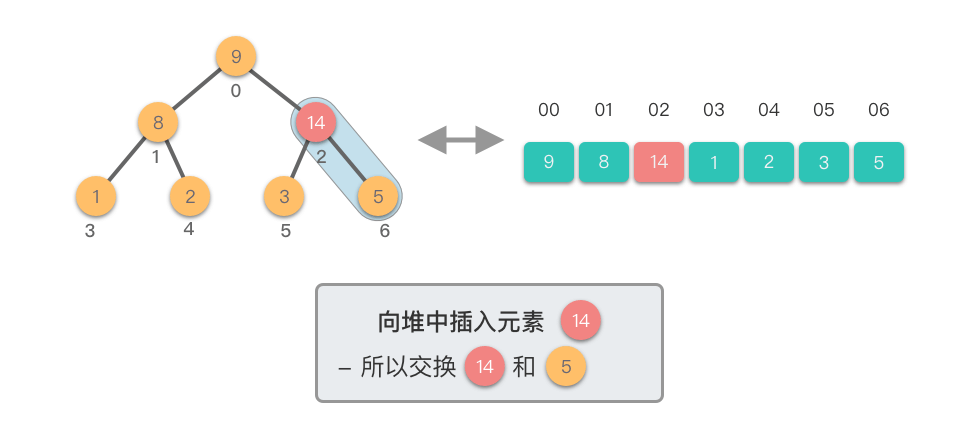
1. 如果新节点的值大于其父节点的值，则交换它们，以保持最大堆的特性。
2. 如果新节点的值小于等于其父节点的值，说明已满足最大堆的特性，此时结束。
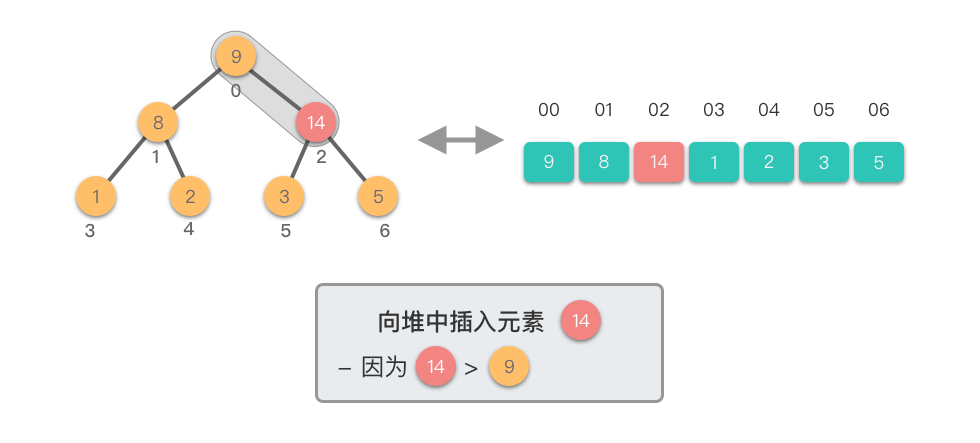
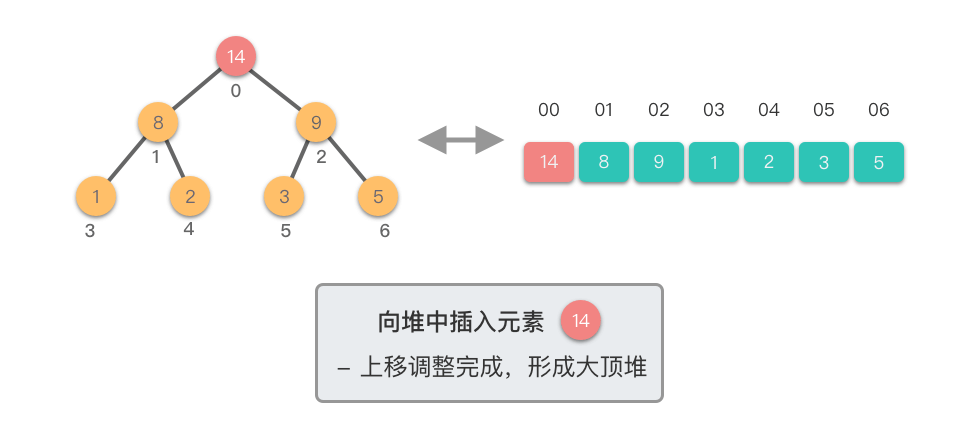
重复上述比较和交换步骤，直到新节点不再大于其父节点，或者达到了堆的根节点。

这个过程称为「上移调整（Shift Up）」。因为新插入的元素会逐步向堆的上方移动，直到找到了合适的位置，保持堆的有序性。

::: tabs#heapPush

@tab <1>

@tab <2>

@tab <3>

@tab <4>

@tab <5>

@tab <6>

@tab <7>

:::

class MaxHeap:
    ......
    def push(self, val: int):
        # 将新元素添加到堆的末尾
        self.max_heap.append(val)
        
        size = len(self.max_heap)
        # 从新插入的元素节点开始，进行上移调整
        self.__shift_up(size - 1)
        
    def __shift_up(self, i: int):
        while (i - 1) // 2 >= 0 and self.max_heap[i] > self.max_heap[(i - 1) // 2]:
            self.max_heap[i], self.max_heap[(i - 1) // 2] = self.max_heap[(i - 1) // 2], self.max_heap[i]
            i = (i - 1) // 2

在最坏情况下，「向堆中插入元素」的时间复杂度为 $O(\log n)$，其中 $n$ 是堆中元素的数量，这是因为堆的高度是 $\log n$。

1.5 删除堆顶元素

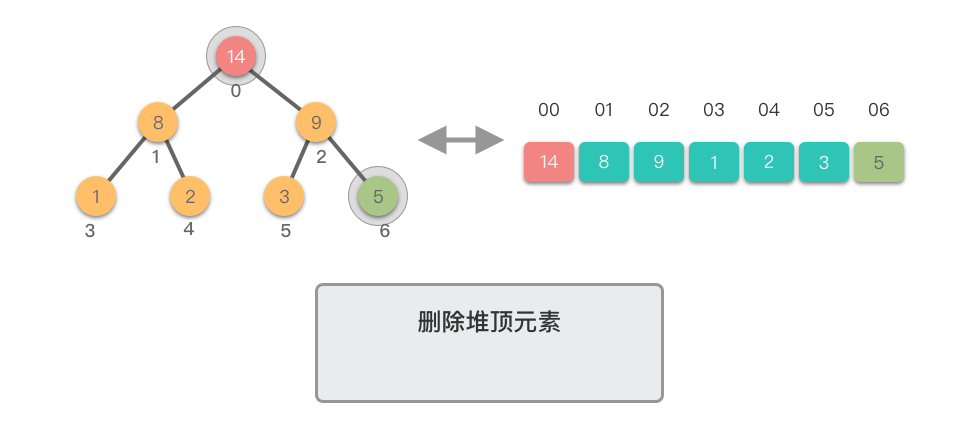
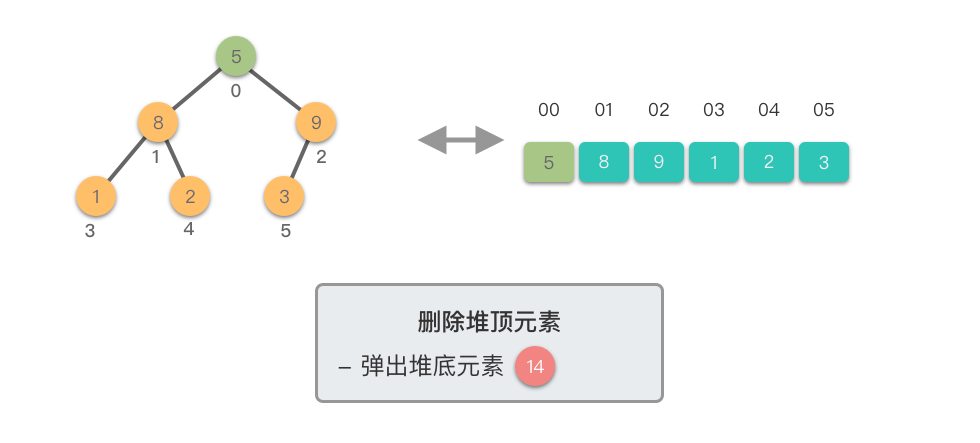
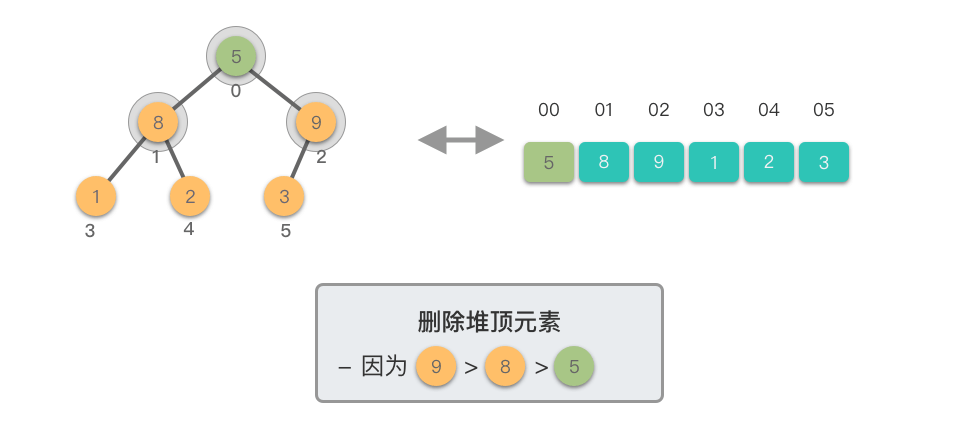
删除堆顶元素：指的是从堆中移除位于堆顶的元素，并重新调整对结果，以保持堆的特性不变。

删除堆顶元素的步骤如下：

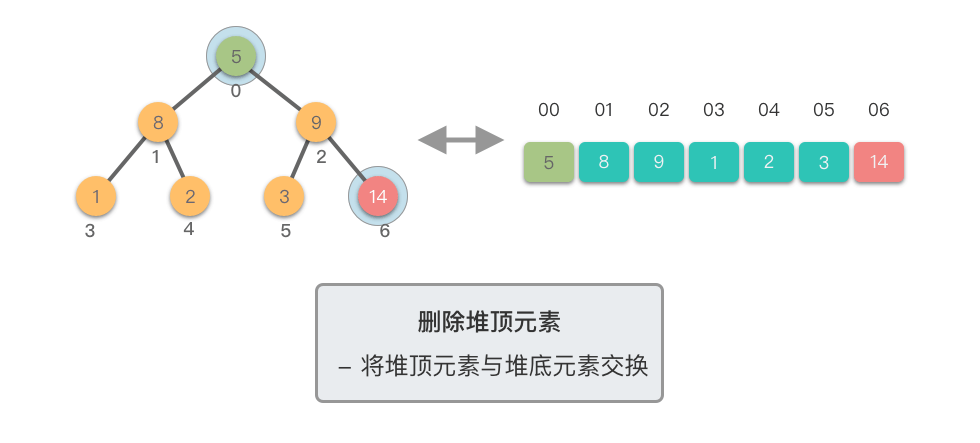
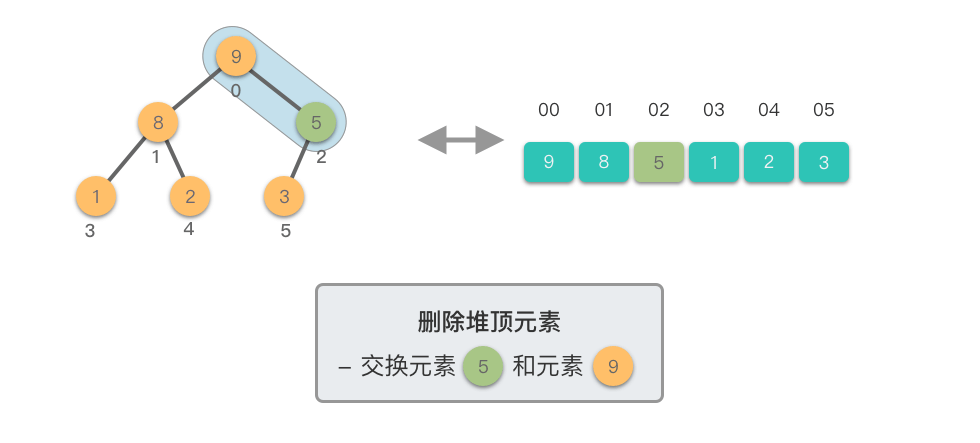
将堆顶元素（即根节点）与堆的末尾元素交换。
移除堆末尾的元素（之前的堆顶），即将其从堆中剔除。
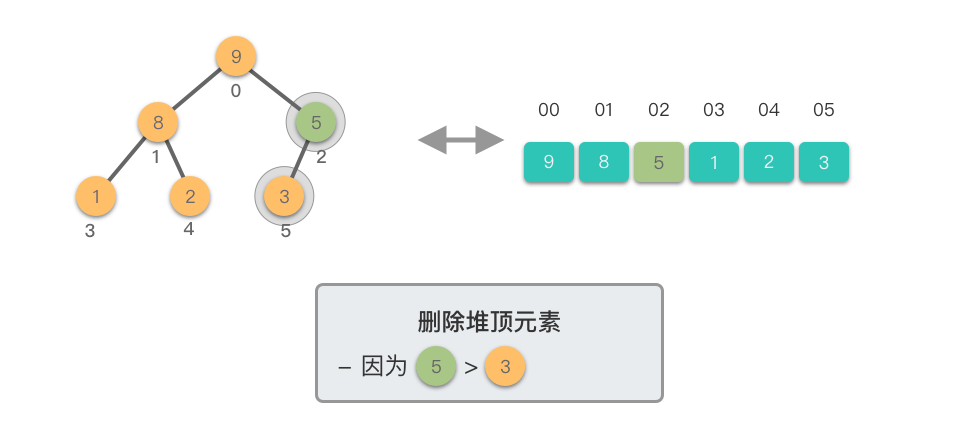
从新的堆顶元素开始，将其与其较大的子节点进行比较。
1. 如果当前节点的值小于其较大的子节点，则将它们交换。这一步是为了将新的堆顶元素「下沉」到适当的位置，以保持最大堆的特性。
2. 如果当前节点的值大于等于其较大的子节点，说明已满足最大堆的特性，此时结束。
重复上述比较和交换步骤，直到新的堆顶元素不再小于其子节点，或者达到了堆的底部。

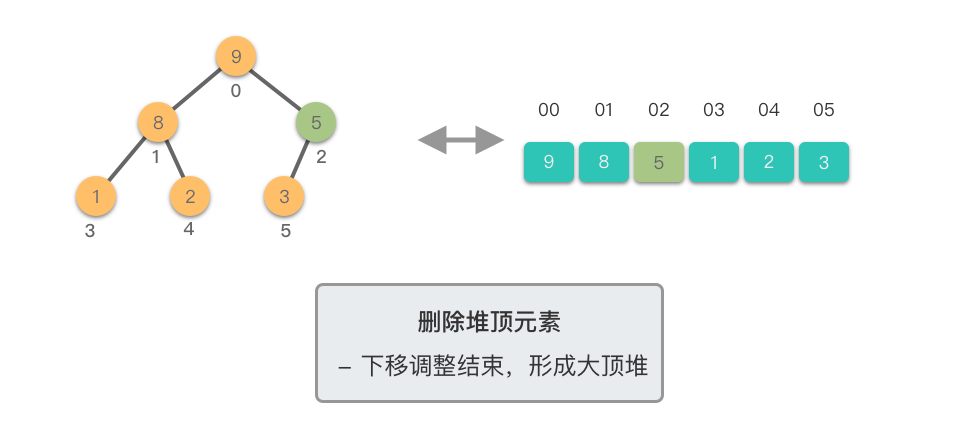
这个过程称为「下移调整（Shift Down）」。因为新的堆顶元素会逐步向堆的下方移动，直到找到了合适的位置，保持堆的有序性。

::: tabs#heapPop

@tab <1>

@tab <2>

@tab <3>

@tab <4>

@tab <5>

@tab <6>

@tab <7>

:::

class MaxHeap:
    ......        
    def pop(self) -> int:
        # 堆为空
        if not self.max_heap:
            raise IndexError("堆为空")
        
        size = len(self.max_heap)
        self.max_heap[0], self.max_heap[size - 1] = self.max_heap[size - 1], self.max_heap[0]
        # 删除堆顶元素
        val = self.max_heap.pop()
        # 节点数减 1
        size -= 1 
        
        # 下移调整
        self.__shift_down(0, size)
        
        # 返回堆顶元素
        return val

    
    def __shift_down(self, i: int, n: int):
        while 2 * i + 1 < n:
            # 左右子节点编号
            left, right = 2 * i + 1, 2 * i + 2
            
            # 找出左右子节点中的较大值节点编号
            if 2 * i + 2 >= n:
                # 右子节点编号超出范围（只有左子节点
                larger = left
            else:
                # 左子节点、右子节点都存在
                if self.max_heap[left] >= self.max_heap[right]:
                    larger = left
                else:
                    larger = right
            
            # 将当前节点值与其较大的子节点进行比较
            if self.max_heap[i] < self.max_heap[larger]:
                # 如果当前节点值小于其较大的子节点，则将它们交换
                self.max_heap[i], self.max_heap[larger] = self.max_heap[larger], self.max_heap[i]
                i = larger
            else:
                # 如果当前节点值大于等于于其较大的子节点，此时结束
                break

「删除堆顶元素」的时间复杂度通常为$O(\log n)$，其中 $n$ 是堆中元素的数量，因为堆的高度是 $\log n$。

2. 堆排序

2.1 堆排序算法思想

堆排序（Heap sort）基本思想：

借用「堆结构」所设计的排序算法。将数组转化为大顶堆，重复从大顶堆中取出数值最大的节点，并让剩余的堆结构继续维持大顶堆性质。

2.2 堆排序算法步骤

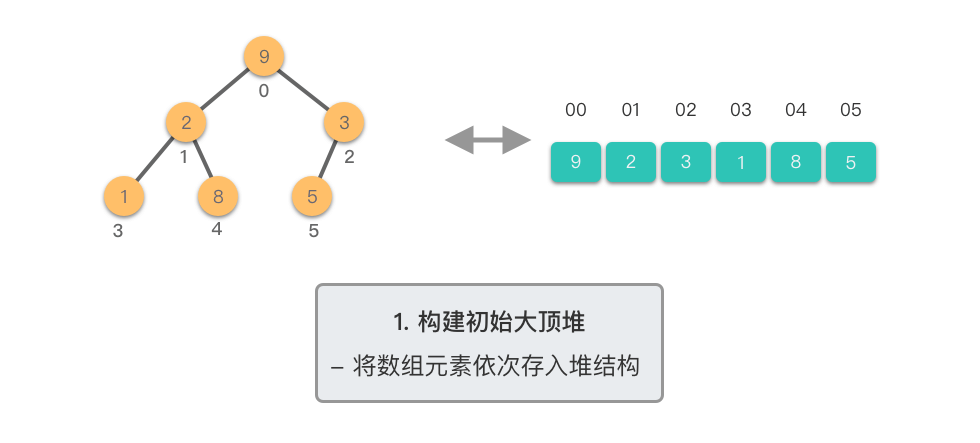
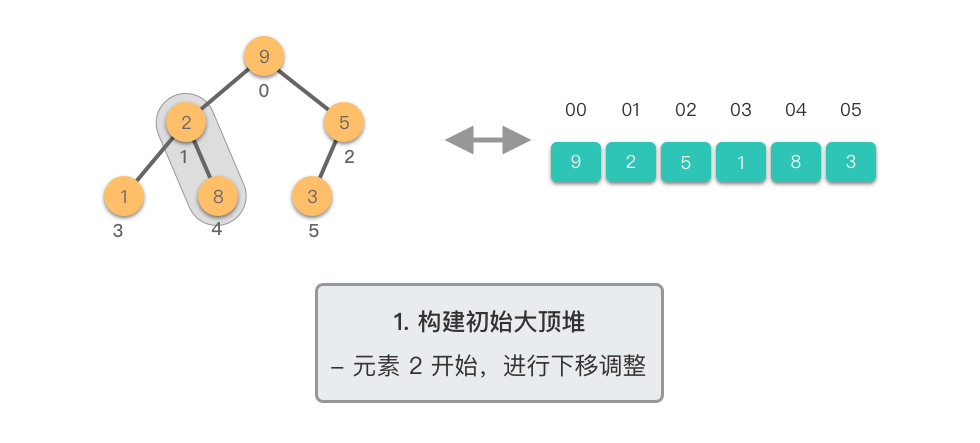
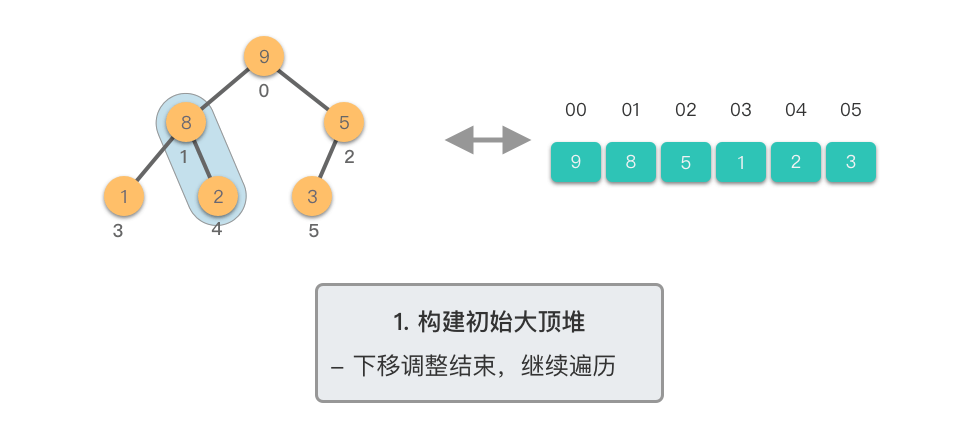
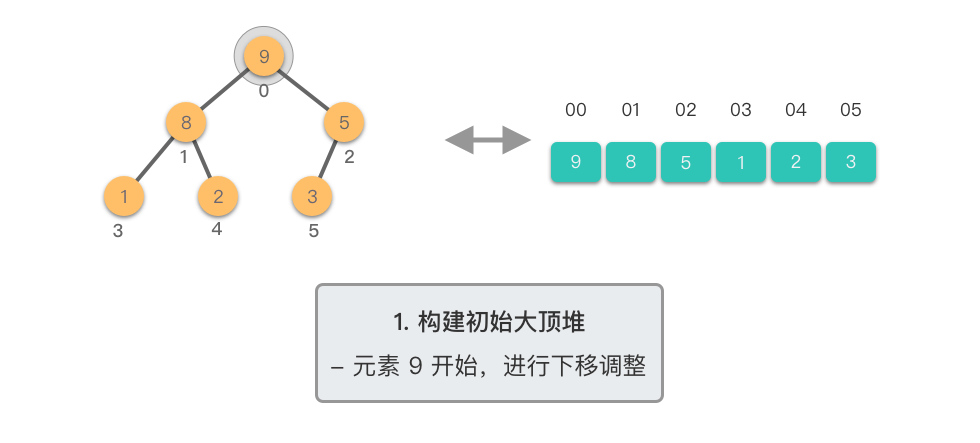
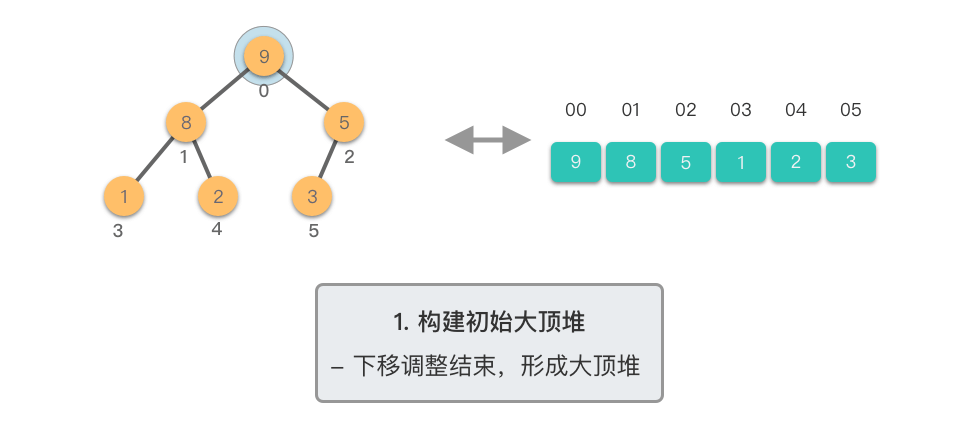
构建初始大顶堆：
1. 定义一个数组实现的堆结构，将原始数组的元素依次存入堆结构的数组中（初始顺序不变）。
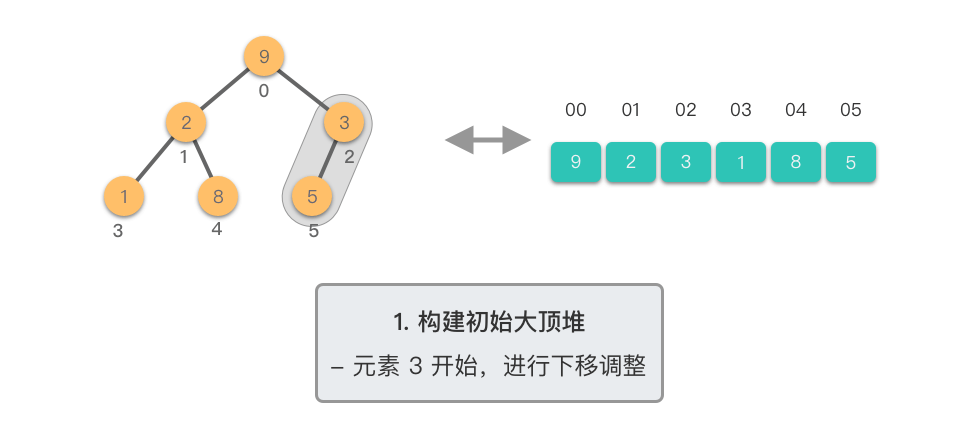
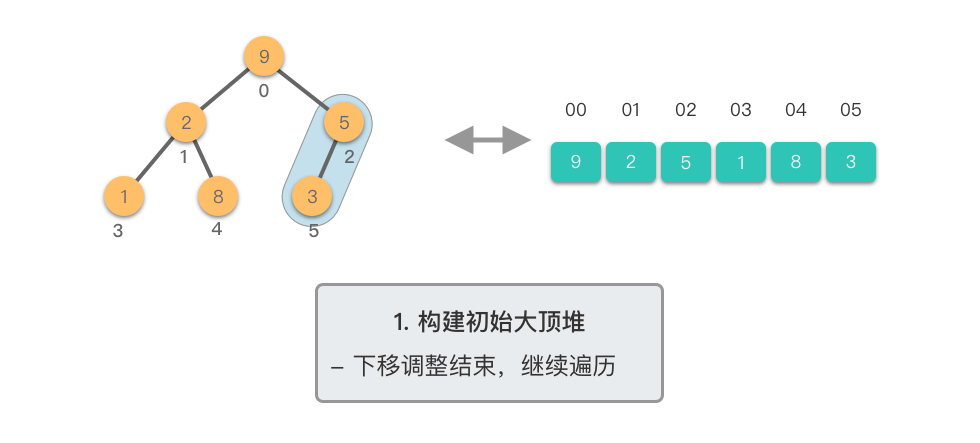
2. 从数组的中间位置开始，从右至左，依次通过「下移调整」将数组转换为一个大顶堆。
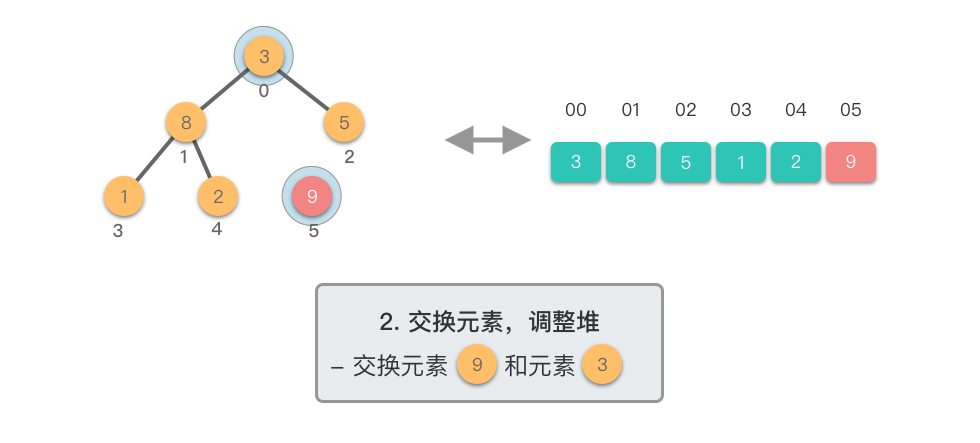
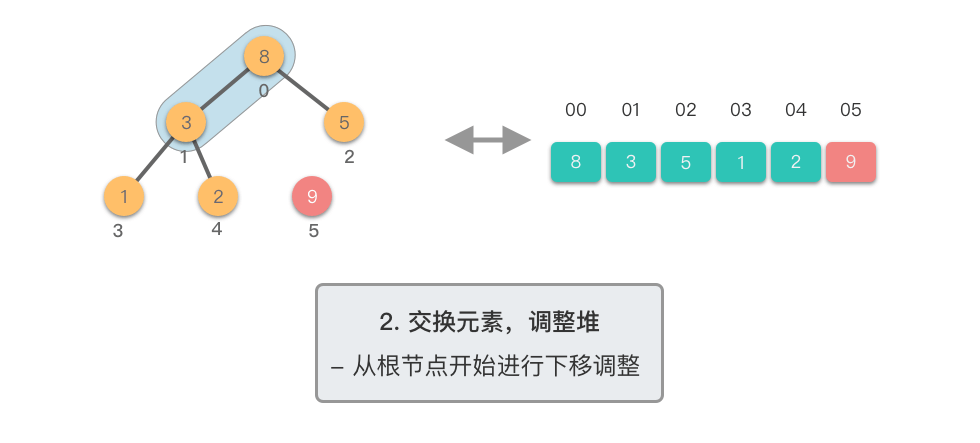
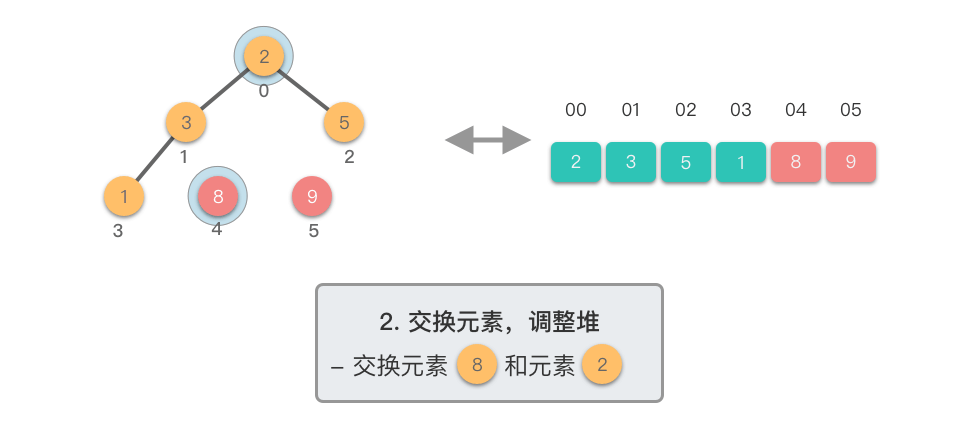
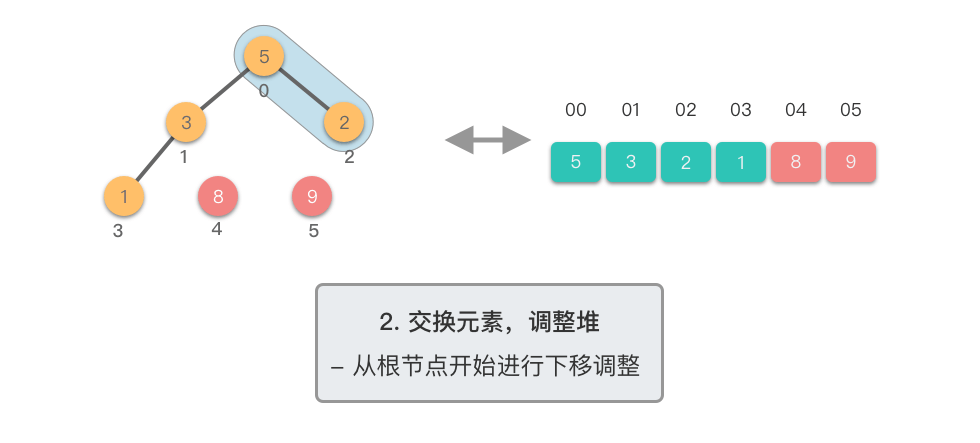
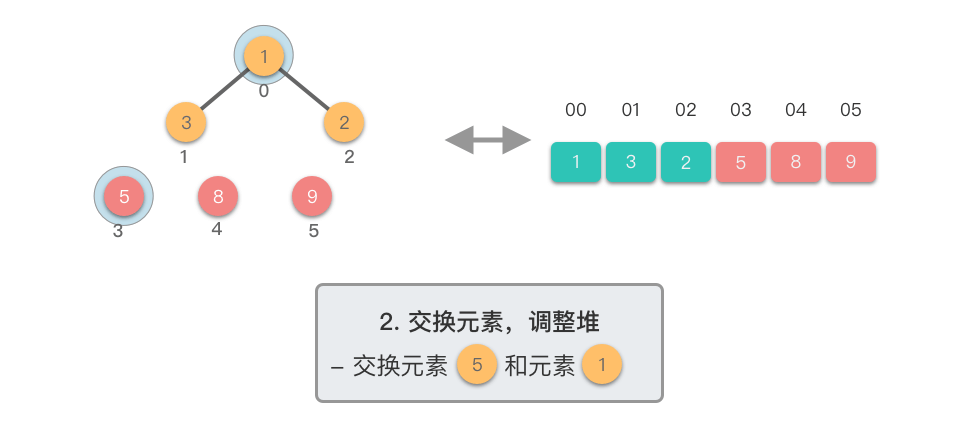
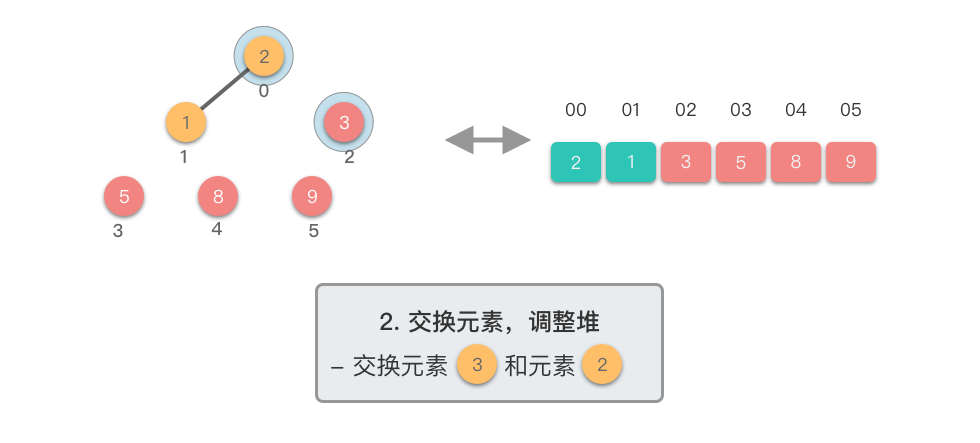
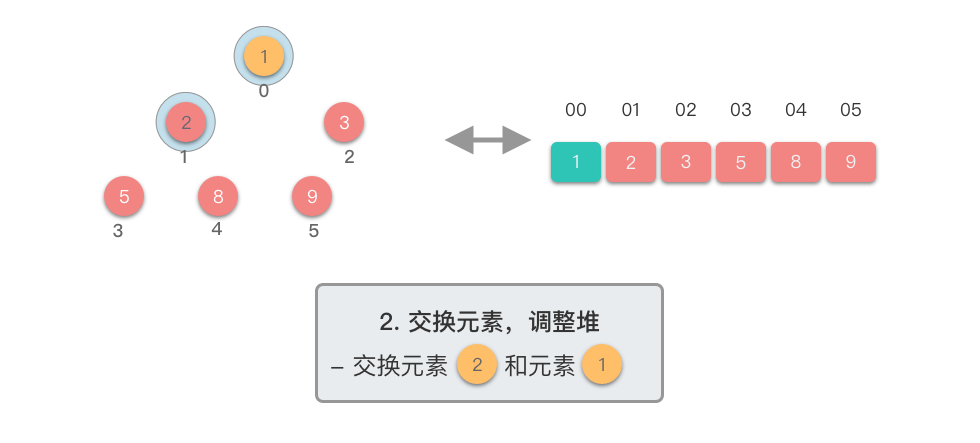
交换元素，调整堆：
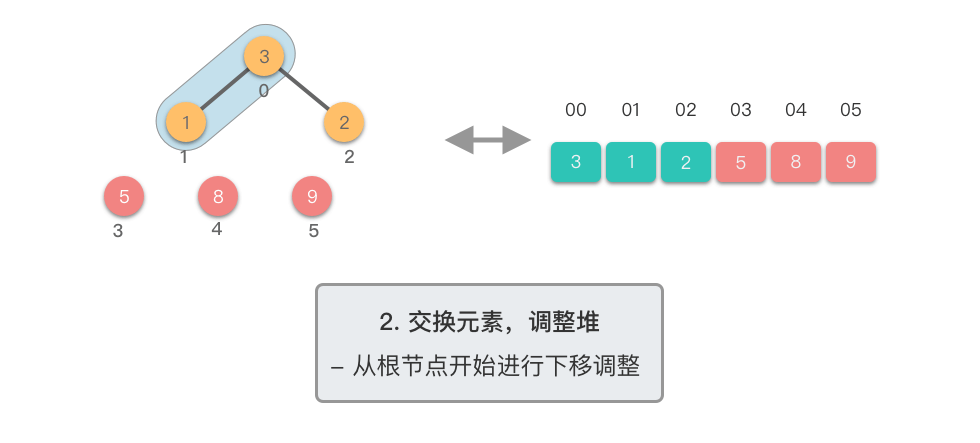
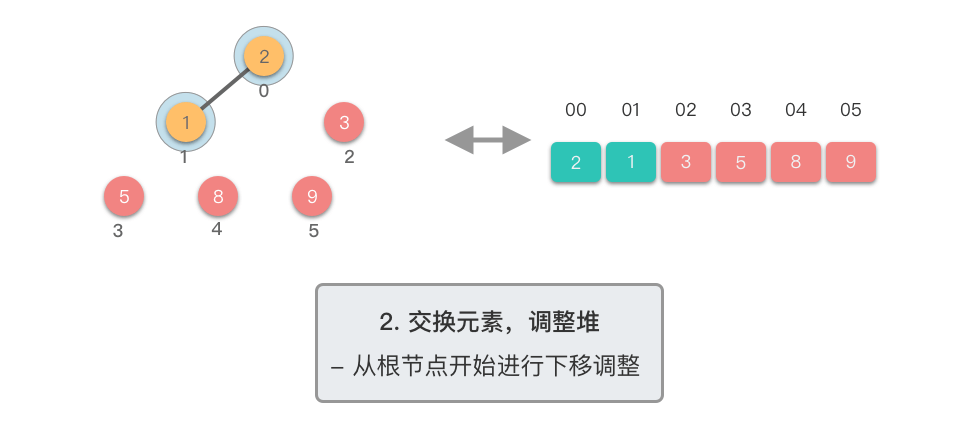
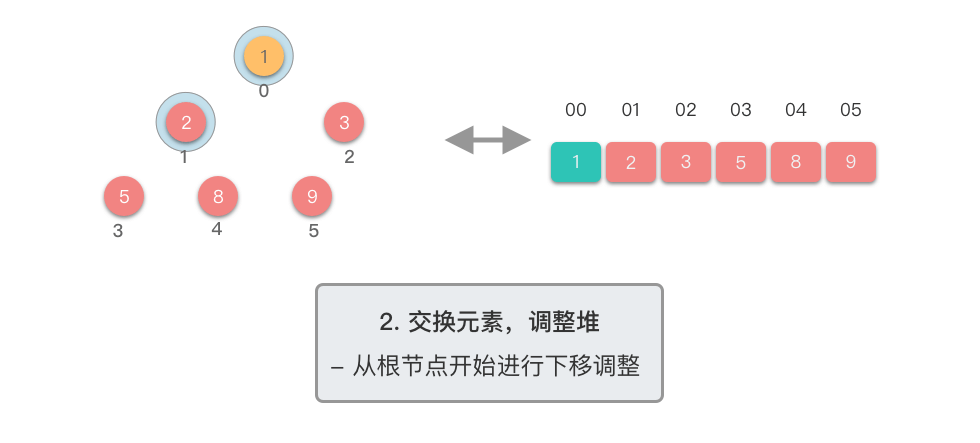
1. 交换堆顶元素（第 $1$ 个元素）与末尾（最后 $1$ 个元素）的位置，交换完成后，堆的长度减 $1$。
2. 交换元素之后，由于堆顶元素发生了改变，需要从根节点开始，对当前堆进行「下移调整」，使其保持堆的特性。
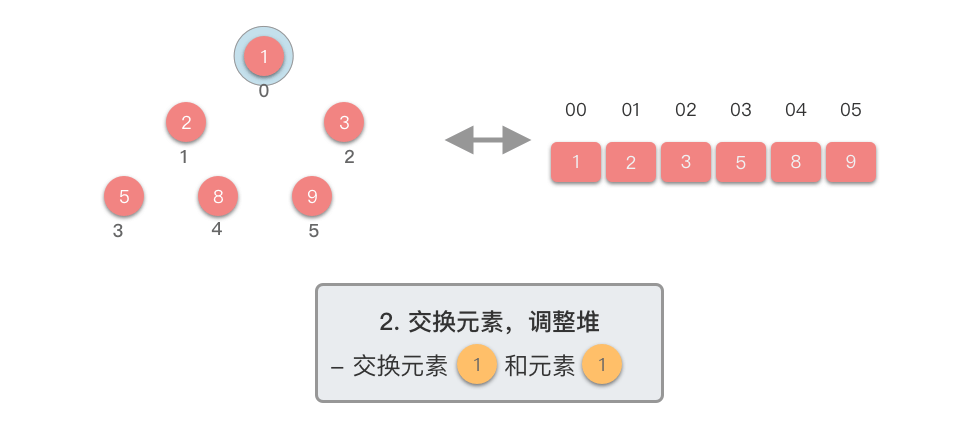
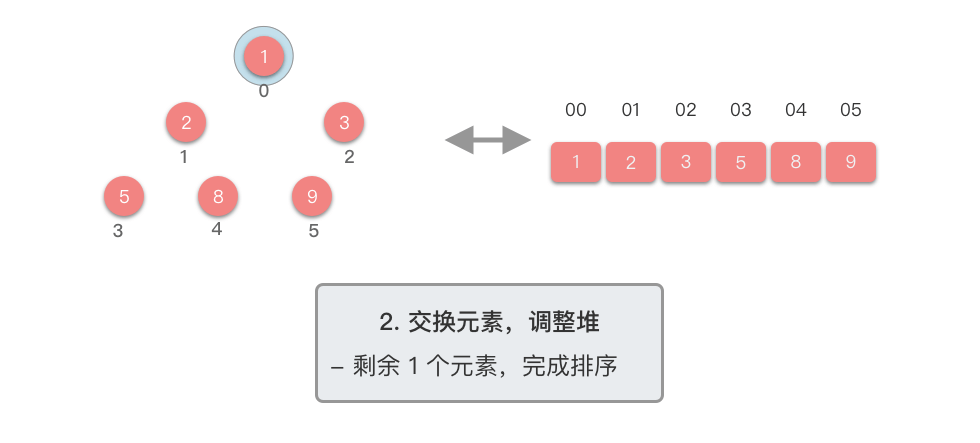
重复交换和调整堆：
1. 重复第 $2$ 步，直到堆的大小为 $1$ 时，此时大顶堆的数组已经完全有序。

::: tabs#heapSortBuildMaxHeap

@tab <1>

@tab <2>

@tab <3>

@tab <4>

@tab <5>

@tab <6>

@tab <7>

:::

::: tabs#heapSortExchangeVal

@tab <1>

@tab <2>

@tab <3>

@tab <4>

@tab <5>

@tab <6>

@tab <7>

@tab <8>

@tab <9>

@tab <10>

@tab <11>

@tab <12>

:::

2.3 堆排序代码实现

class MaxHeap:
    ......
    def __buildMaxHeap(self, nums: [int]):
        size = len(nums)
        # 先将数组 nums 的元素按顺序添加到 max_heap 中
        for i in range(size):
            self.max_heap.append(nums[i])
        
        # 从最后一个非叶子节点开始，进行下移调整
        for i in range((size - 2) // 2, -1, -1):
            self.__shift_down(i, size)

    def maxHeapSort(self, nums: [int]) -> [int]:
        # 根据数组 nums 建立初始堆
        self.__buildMaxHeap(nums)
        
        size = len(self.max_heap)
        for i in range(size - 1, -1, -1):
            # 交换根节点与当前堆的最后一个节点
            self.max_heap[0], self.max_heap[i] = self.max_heap[i], self.max_heap[0]
            # 从根节点开始，对当前堆进行下移调整
            self.__shift_down(0, i)
        
        # 返回排序后的数组
        return self.max_heap
    
class Solution:
    def maxHeapSort(self, nums: [int]) -> [int]:
        return MaxHeap().maxHeapSort(nums)
        
    def sortArray(self, nums: [int]) -> [int]:
        return self.maxHeapSort(nums)
    
print(Solution().sortArray([10, 25, 6, 8, 7, 1, 20, 23, 16, 19, 17, 3, 18, 14]))

2.4 堆排序算法分析

时间复杂度：$O(n \times \log n)$。
- 堆积排序的时间主要花费在两个方面：「建立初始堆」和「下移调整」。
- 设原始数组所对应的完全二叉树深度为 $d$，算法由两个独立的循环组成：
  1. 在第 $1$ 个循环构造初始堆积时，从 $i = d - 1$ 层开始，到 $i = 1$ 层为止，对每个分支节点都要调用一次调整堆算法，而一次调整堆算法，对于第 $i$ 层一个节点到第 $d$ 层上建立的子堆积，所有节点可能移动的最大距离为该子堆积根节点移动到最后一层（第 $d$ 层）的距离，即 $d - i$。而第 $i$ 层上节点最多有 $2^{i-1}$ 个，所以每一次调用调整堆算法的最大移动距离为 $2^{i-1} * (d-i)$。因此，堆积排序算法的第 $1$ 个循环所需时间应该是各层上的节点数与该层上节点可移动的最大距离之积的总和，即：$\sum_{i = d - 1}^1 2^{i-1} (d-i) = \sum_{j = 1}^{d-1} 2^{d-j-1} \times j = \sum_{j = 1}^{d-1} 2^{d-1} \times {j \over 2^j} \le n \times \sum_{j = 1}^{d-1} {j \over 2^j} < 2 \times n$。这一部分的时间花费为 $O(n)$。
  2. 在第 $2$ 个循环中，每次调用调整堆算法一次，节点移动的最大距离为这棵完全二叉树的深度 $d = \lfloor \log_2(n) \rfloor + 1$，一共调用了 $n - 1$ 次调整堆算法，所以，第 $2$ 个循环的时间花费为 $(n-1)(\lfloor \log_2 (n)\rfloor + 1) = O(n \times \log n)$。
- 因此，堆积排序的时间复杂度为 $O(n \times \log n)$。
空间复杂度：$O(1)$。由于在堆积排序中只需要一个记录大小的辅助空间，因此，堆积排序的空间复杂度为：$O(1)$。
排序稳定性：在进行「下移调整」时，相等元素的相对位置可能会发生变化。因此，堆排序是一种 不稳定排序算法。

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

07.Array-Heap-Sort.md

07.Array-Heap-Sort.md

1. 堆结构

1.1 堆的定义

1.2 堆的存储结构

1.3 访问堆顶元素

1.4 向堆中插入元素

1.5 删除堆顶元素

2. 堆排序

2.1 堆排序算法思想

2.2 堆排序算法步骤

2.3 堆排序代码实现

2.4 堆排序算法分析

Files

07.Array-Heap-Sort.md

Latest commit

History

07.Array-Heap-Sort.md

File metadata and controls

1. 堆结构

1.1 堆的定义

1.2 堆的存储结构

1.3 访问堆顶元素

1.4 向堆中插入元素

1.5 删除堆顶元素

2. 堆排序

2.1 堆排序算法思想

2.2 堆排序算法步骤

2.3 堆排序代码实现

2.4 堆排序算法分析