01.Array-Bubble-Sort.md

1. 冒泡排序算法思想

冒泡排序（Bubble Sort）基本思想：

经过多次迭代，通过相邻元素之间的比较与交换，使值较小的元素逐步从后面移到前面，值较大的元素从前面移到后面。

这个过程就像水底的气泡一样从底部向上「冒泡」到水面，这也是冒泡排序法名字的由来。

接下来，我们使用「冒泡」的方式来模拟一下这个过程。

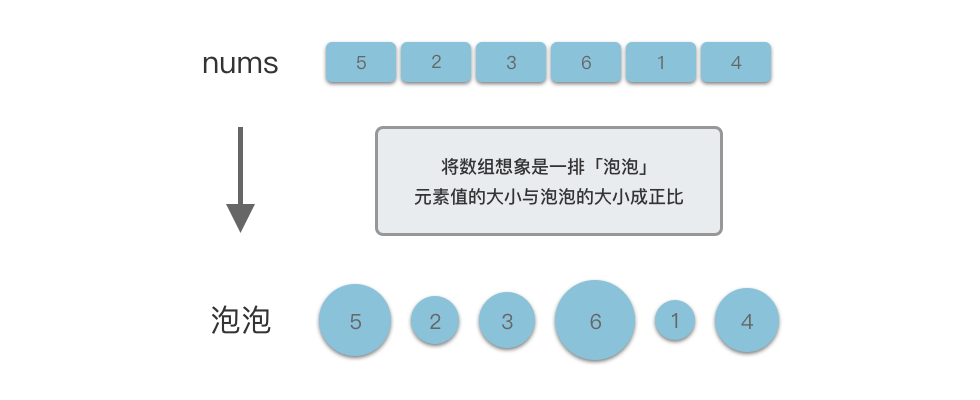
1. 首先将数组想象是一排「泡泡」，元素值的大小与泡泡的大小成正比。
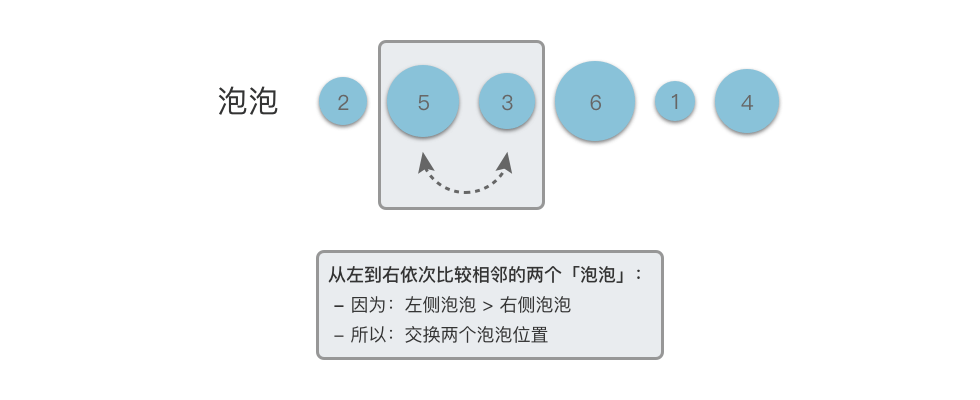
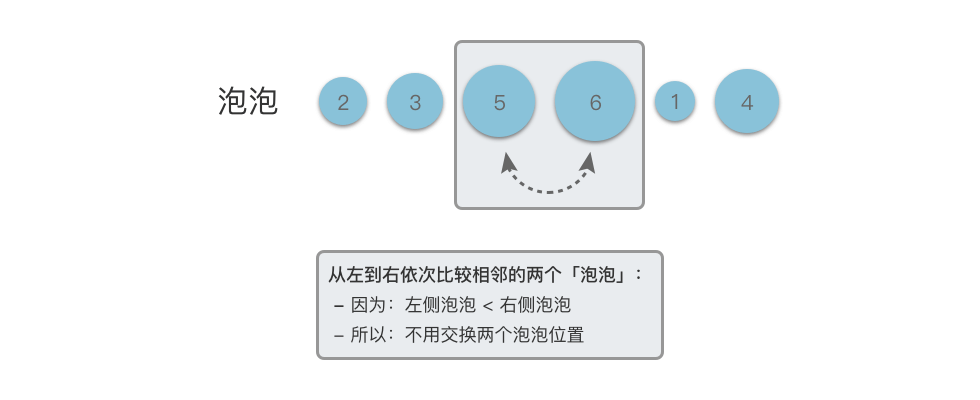
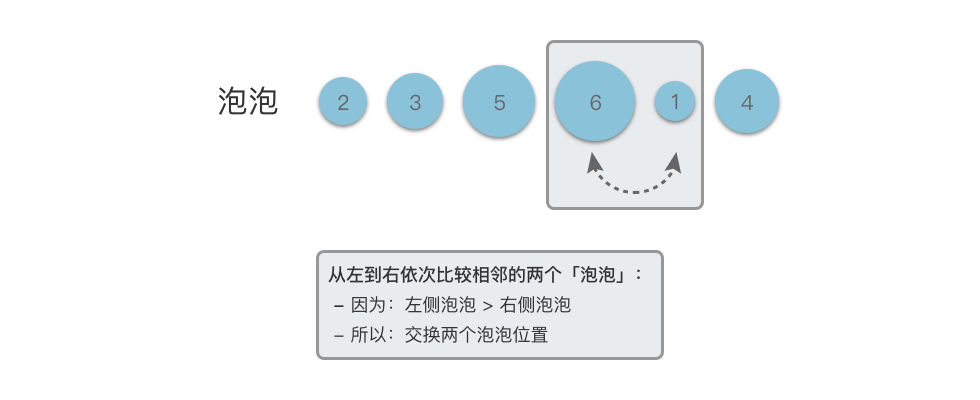
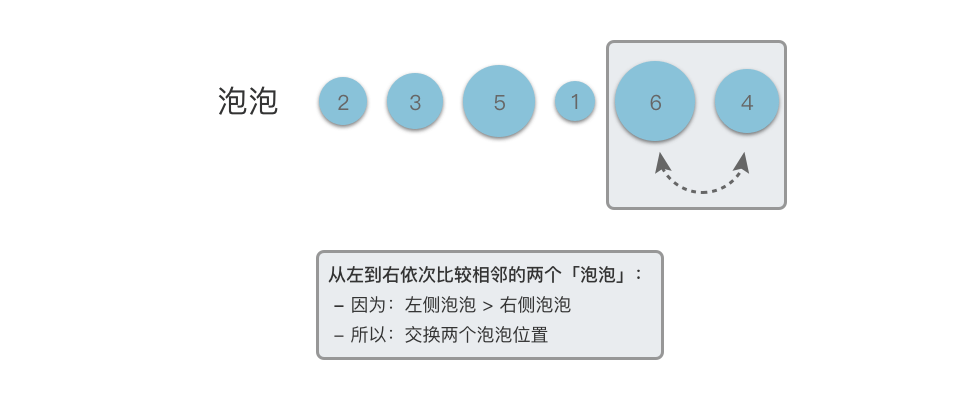
2. 然后从左到右依次比较相邻的两个「泡泡」：
   1. 如果左侧泡泡大于右侧泡泡，则交换两个泡泡的位置。
   2. 如果左侧泡泡小于等于右侧泡泡，则两个泡泡保持不变。
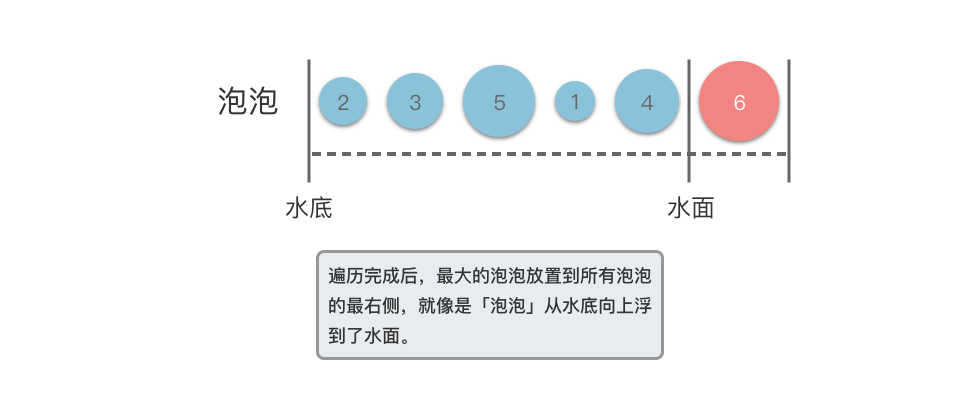
3. 这 $1$ 趟遍历完成之后，最大的泡泡就会放置到所有泡泡的最右侧，就像是「泡泡」从水底向上浮到了水面。

::: tabs#bubble

@tab <1>

@tab <2>

@tab <3>

@tab <4>

@tab <5>

@tab <6>

@tab <7>

:::

2. 冒泡排序算法步骤

假设数组的元素个数为 $n$ 个，则冒泡排序的算法步骤如下：

1. 第 $1$ 趟「冒泡」：对前 $n$ 个元素执行「冒泡」，从而使第 $1$ 个值最大的元素放置在正确位置上。
   1. 先将序列中第 $1$ 个元素与第 $2$ 个元素进行比较，如果前者大于后者，则两者交换位置，否则不交换。
   2. 然后将第 $2$ 个元素与第 $3$ 个元素比较，如果前者大于后者，则两者交换位置，否则不交换。
   3. 依次类推，直到第 $n - 1$ 个元素与第 $n$ 个元素比较（或交换）为止。
   4. 经过第 $1$ 趟排序，使得 $n$ 个元素中第 $i$ 个值最大元素被安置在第 $n$ 个位置上。
2. 第 $2$ 趟「冒泡」：对前 $n - 1$ 个元素执行「冒泡」，从而使第 $2$ 个值最大的元素放置在正确位置上。
   1. 先将序列中第 $1$ 个元素与第 $2$ 个元素进行比较，若前者大于后者，则两者交换位置，否则不交换。
   2. 然后将第 $2$ 个元素与第 $3$ 个元素比较，若前者大于后者，则两者交换位置，否则不交换。
   3. 依次类推，直到对 $n - 2$ 个元素与第 $n - 1$ 个元素比较（或交换）为止。
   4. 经过第 $2$ 趟排序，使得数组中第 $2$ 个值最大元素被安置在第 $n$ 个位置上。
3. 依次类推，重复上述「冒泡」过程，直到某一趟排序过程中不出现元素交换位置的动作，则排序结束。

我们以 $[5, 2, 3, 6, 1, 4]$ 为例，演示一下冒泡排序算法的整个步骤。

3. 冒泡排序代码实现

class Solution:
    def bubbleSort(self, nums: [int]) -> [int]:
        # 第 i 趟「冒泡」
        for i in range(len(nums) - 1):
            flag = False    # 是否发生交换的标志位
            # 从数组中前 n - i + 1 个元素的第 1 个元素开始，相邻两个元素进行比较
            for j in range(len(nums) - i - 1):
                # 相邻两个元素进行比较，如果前者大于后者，则交换位置
                if nums[j] > nums[j + 1]:
                    nums[j], nums[j + 1] = nums[j + 1], nums[j]
                    flag = True
            if not flag:    # 此趟遍历未交换任何元素，直接跳出
                break
        
        return nums
    
    def sortArray(self, nums: [int]) -> [int]:
        return self.bubbleSort(nums)

4. 冒泡排序算法分析

• 最佳时间复杂度：$O(n)$。最好的情况下（初始时序列已经是升序排列），只需经过 $1$ 趟排序，总共经过 $n$ 次元素之间的比较，并且不移动元素，算法就可以结束排序。因此，冒泡排序算法的最佳时间复杂度为 $O(n)$。
• 最坏时间复杂度：$O(n^2)$。最差的情况下（初始时序列已经是降序排列，或者最小值元素处在序列的最后），则需要进行 $n$ 趟排序，总共进行 $∑^n_{i=2}(i−1) = \frac{n(n−1)}{2}$ 次元素之间的比较，因此，冒泡排序算法的最坏时间复杂度为 $O(n^2)$。
• 空间复杂度：$O(1)$。冒泡排序为原地排序算法，只用到指针变量 $i$、$j$ 以及标志位 $flag$ 等常数项的变量。
• 冒泡排序适用情况：冒泡排序方法在排序过程中需要移动较多次数的元素，并且排序时间效率比较低。因此，冒泡排序方法比较适合于参加排序序列的数据量较小的情况，尤其是当序列的初始状态为基本有序的情况。
• 排序稳定性：由于元素交换是在相邻元素之间进行的，不会改变相等元素的相对顺序，因此，冒泡排序法是一种 稳定排序算法。

参考资料

• 【文章】11.3. 冒泡排序 - Hello 算法