参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
提示:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 300
- grid[i][j] 的值为 '0' 或 '1'
注意题目中每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
这道题题目是 DFS,BFS,并查集,基础题目。
本题思路,是用遇到一个没有遍历过的节点陆地,计数器就加一,然后把该节点陆地所能遍历到的陆地都标记上。
在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。
那么如果把节点陆地所能遍历到的陆地都标记上呢,就可以使用 DFS,BFS或者并查集。
不少同学用广搜做这道题目的时候,超时了。 这里有一个广搜中很重要的细节:
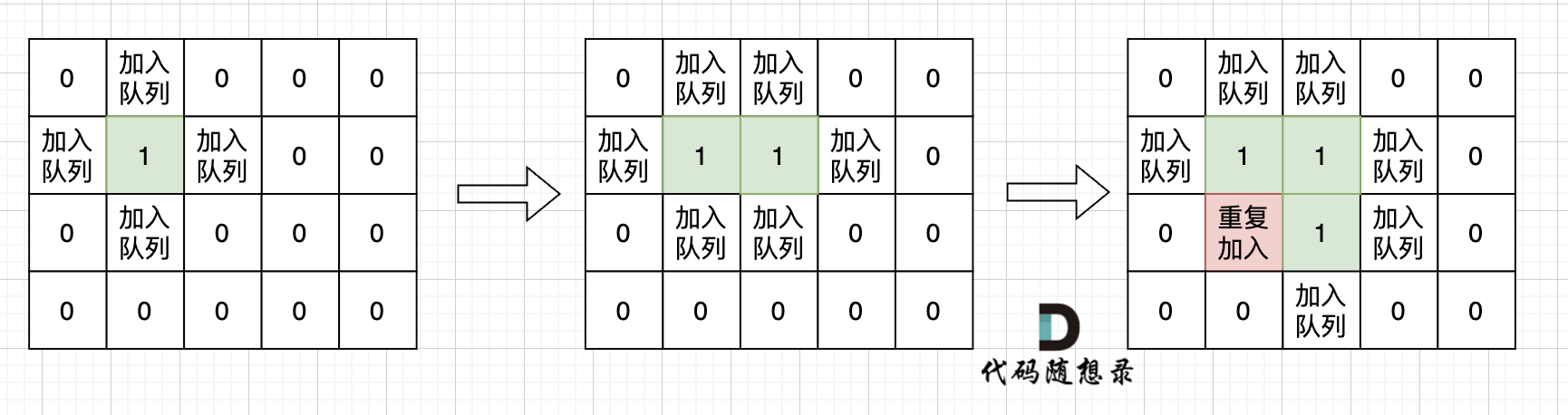
根本原因是只要 加入队列就代表 走过,就需要标记,而不是从队列拿出来的时候再去标记走过。
很多同学可能感觉这有区别吗?
如果从队列拿出节点,再去标记这个节点走过,就会发生下图所示的结果,会导致很多节点重复加入队列。
超时写法 (从队列中取出节点再标记)
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
visited[curx][cury] = true; // 从队列中取出在标记走过
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
que.push({nextx, nexty});
}
}
}
}加入队列 就代表走过,立刻标记,正确写法:
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
visited[x][y] = true; // 只要加入队列,立刻标记
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
que.push({nextx, nexty});
visited[nextx][nexty] = true; // 只要加入队列立刻标记
}
}
}
}以上两个版本其实,其实只有细微区别,就是 visited[x][y] = true; 放在的地方,着去取决于我们对 代码中队列的定义,队列中的节点就表示已经走过的节点。 所以只要加入队列,立即标记该节点走过。
本题完整广搜代码:
class Solution {
private:
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
visited[x][y] = true; // 只要加入队列,立刻标记
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
que.push({nextx, nexty});
visited[nextx][nexty] = true; // 只要加入队列立刻标记
}
}
}
}
public:
int numIslands(vector<vector<char>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == '1') {
result++; // 遇到没访问过的陆地,+1
bfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
}
}
}
return result;
}
};
class Solution {
boolean[][] visited;
int[][] move = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public int numIslands(char[][] grid) {
int res = 0;
visited = new boolean[grid.length][grid[0].length];
for(int i = 0; i < grid.length; i++) {
for(int j = 0; j < grid[0].length; j++) {
if(!visited[i][j] && grid[i][j] == '1') {
bfs(grid, i, j);
res++;
}
}
}
return res;
}
//将这片岛屿上的所有陆地都访问到
public void bfs(char[][] grid, int y, int x) {
Deque<int[]> queue = new ArrayDeque<>();
queue.offer(new int[]{y, x});
visited[y][x] = true;
while(!queue.isEmpty()) {
int[] cur = queue.poll();
int m = cur[0];
int n = cur[1];
for(int i = 0; i < 4; i++) {
int nexty = m + move[i][0];
int nextx = n + move[i][1];
if(nextx < 0 || nexty == grid.length || nexty < 0 || nextx == grid[0].length) continue;
if(!visited[nexty][nextx] && grid[nexty][nextx] == '1') {
queue.offer(new int[]{nexty, nextx});
visited[nexty][nextx] = true; //只要加入队列就标记为访问
}
}
}
}
}BFS solution
class Solution:
def __init__(self):
self.dirs = [[0, 1], [1, 0], [-1, 0], [0, -1]]
def numIslands(self, grid: List[List[str]]) -> int:
m = len(grid)
n = len(grid[0])
visited = [[False]*n for _ in range(m)]
res = 0
for i in range(m):
for j in range(n):
if visited[i][j] == False and grid[i][j] == '1':
res += 1
self.bfs(grid, i, j, visited) # Call bfs within this condition
return res
def bfs(self, grid, i, j, visited):
q = deque()
q.append((i,j))
visited[i][j] = True
while q:
x, y = q.popleft()
for k in range(4):
next_i = x + self.dirs[k][0]
next_j = y + self.dirs[k][1]
if next_i < 0 or next_i >= len(grid):
continue
if next_j < 0 or next_j >= len(grid[0]):
continue
if visited[next_i][next_j]:
continue
if grid[next_i][next_j] == '0':
continue
q.append((next_i, next_j))
visited[next_i][next_j] = True