例行每周小结
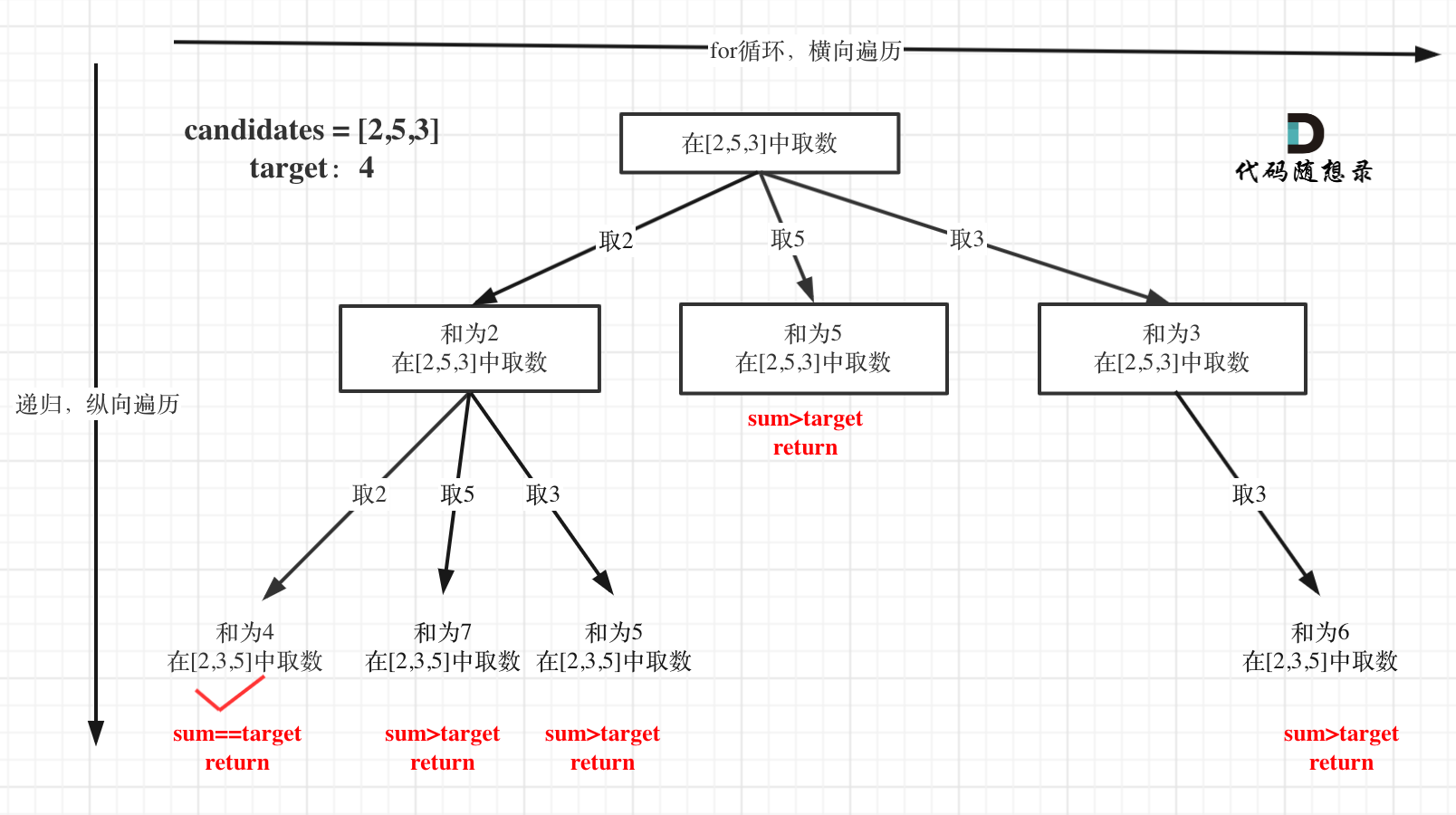
在回溯算法:求组合总和(二)中讲解的组合总和问题,和以前的组合问题还都不一样。
本题和回溯算法:求组合问题!,回溯算法:求组合总和!和区别是:本题没有数量要求,可以无限重复,但是有总和的限制,所以间接的也是有个数的限制。
不少录友都是看到可以重复选择,就义无反顾的把startIndex去掉了。
本题还需要startIndex来控制for循环的起始位置,对于组合问题,什么时候需要startIndex呢?
我举过例子,如果是一个集合来求组合的话,就需要startIndex,例如:回溯算法:求组合问题!,回溯算法:求组合总和!。
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:回溯算法:电话号码的字母组合
注意以上我只是说求组合的情况,如果是排列问题,又是另一套分析的套路,后面我在讲解排列的时候会重点介绍。
最后还给出了本题的剪枝优化,如下:
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++)
这个优化如果是初学者的话并不容易想到。
在求和问题中,排序之后加剪枝是常见的套路!
在回溯算法:求组合总和(二)第一个树形结构没有画出startIndex的作用,这里这里纠正一下,准确的树形结构如图所示:
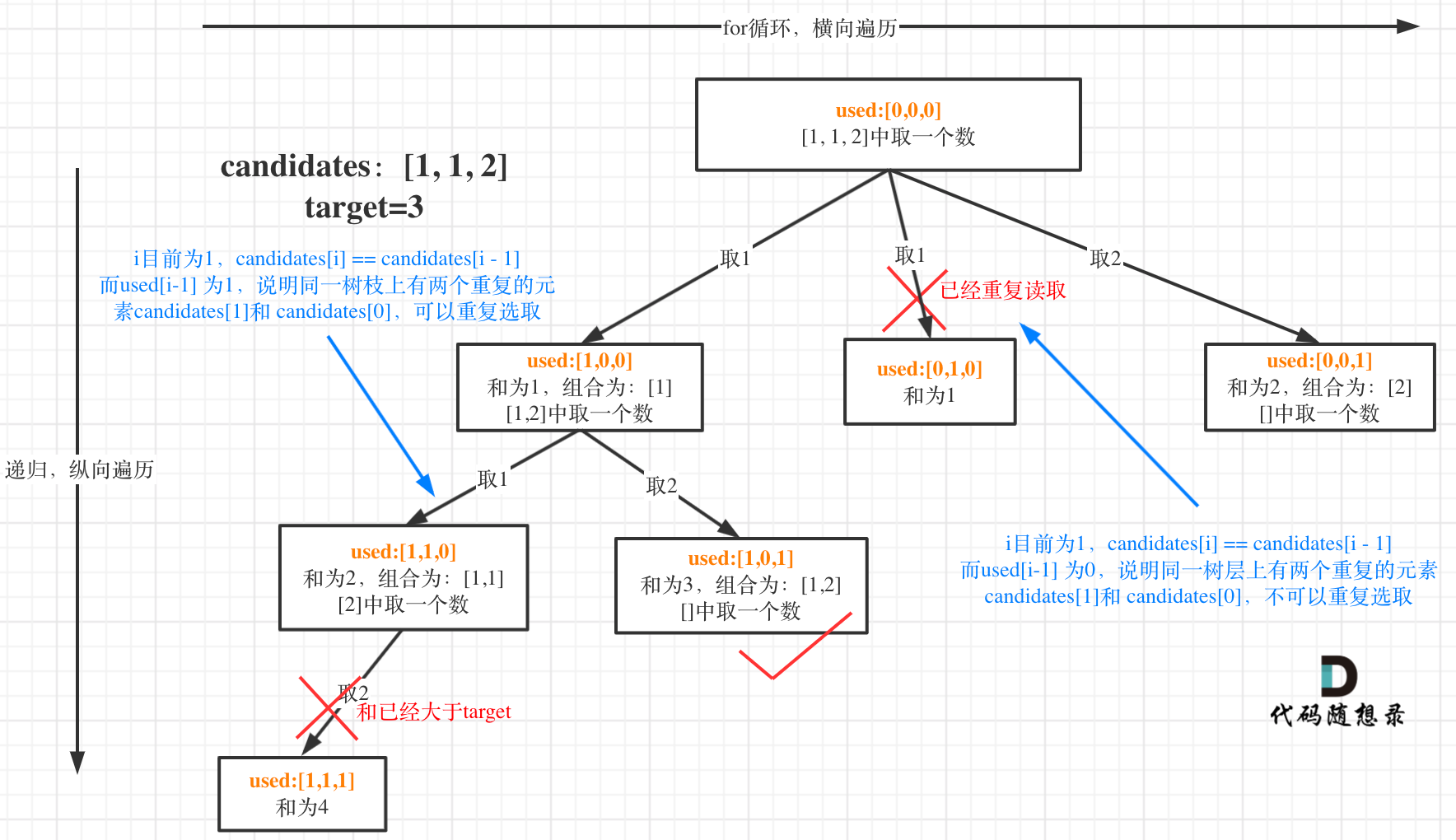
在回溯算法:求组合总和(三)中依旧讲解组合总和问题,本题集合元素会有重复,但要求解集不能包含重复的组合。
所以难就难在去重问题上了。
这个去重问题,相信做过的录友都知道有多么的晦涩难懂。网上的题解一般就说“去掉重复”,但说不清怎么个去重,代码一甩就完事了。
为了讲解这个去重问题,我自创了两个词汇,“树枝去重”和“树层去重”。
都知道组合问题可以抽象为树形结构,那么“使用过”在这个树形结构上是有两个维度的,一个维度是同一树枝上“使用过”,一个维度是同一树层上“使用过”。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。
我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
- used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
- used[i - 1] == false,说明同一树层candidates[i - 1]使用过
这块去重的逻辑很抽象,网上搜的题解基本没有能讲清楚的,如果大家之前思考过这个问题或者刷过这道题目,看到这里一定会感觉通透了很多!
对于去重,其实排列问题也是一样的道理,后面我会讲到。
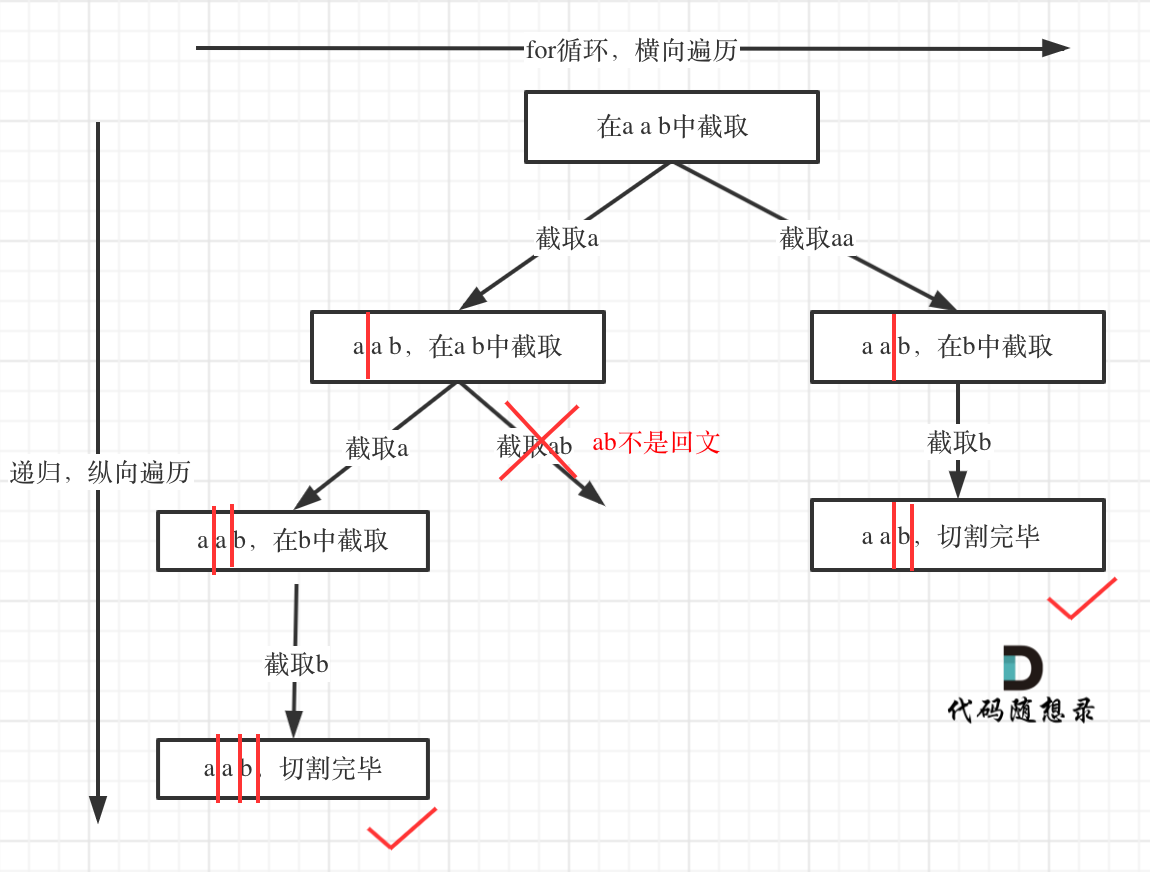
在回溯算法:分割回文串中,我们开始讲解切割问题,虽然最后代码看起来好像是一道模板题,但是从分析到学会套用这个模板,是比较难的。
我列出如下几个难点:
- 切割问题其实类似组合问题
- 如何模拟那些切割线
- 切割问题中递归如何终止
- 在递归循环中如何截取子串
- 如何判断回文
如果想到了用求解组合问题的思路来解决 切割问题本题就成功一大半了,接下来就可以对着模板照葫芦画瓢。
但后序如何模拟切割线,如何终止,如何截取子串,其实都不好想,最后判断回文算是最简单的了。
除了这些难点,本题还有细节,例如:切割过的地方不能重复切割所以递归函数需要传入i + 1。
所以本题应该是一个道hard题目了。
本题的树形结构中,和代码的逻辑有一个小出入,已经判断不是回文的子串就不会进入递归了,纠正如下:
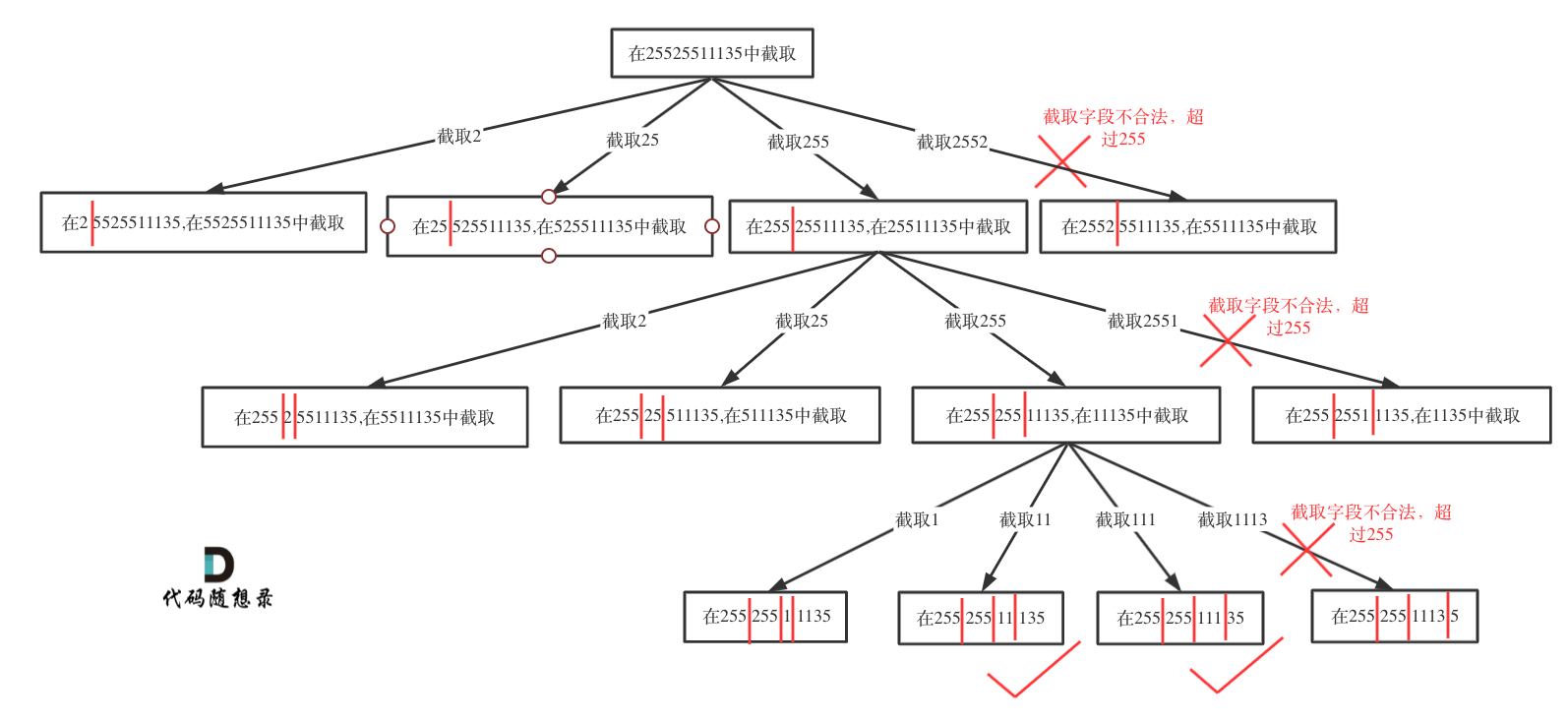
如果没有做过回溯算法:分割回文串的话,回溯算法:复原IP地址这道题目应该是比较难的。
复原IP照回溯算法:分割回文串就多了一些限制,例如只能分四段,而且还是更改字符串,插入逗点。
树形图如下:
在本文的树形结构图中,我已经把详细的分析思路都画了出来,相信大家看了之后一定会思路清晰不少!
本题还可以有一个剪枝,合法ip长度为12,如果s的长度超过了12就不是有效IP地址,直接返回!
代码如下:
if (s.size() > 12) return result; // 剪枝
我之前给出的C++代码没有加这个限制,也没有超时,因为在第四段超过长度之后,就会截止了,所以就算给出特别长的字符串,搜索的范围也是有限的(递归只会到第三层),及时就会返回了。
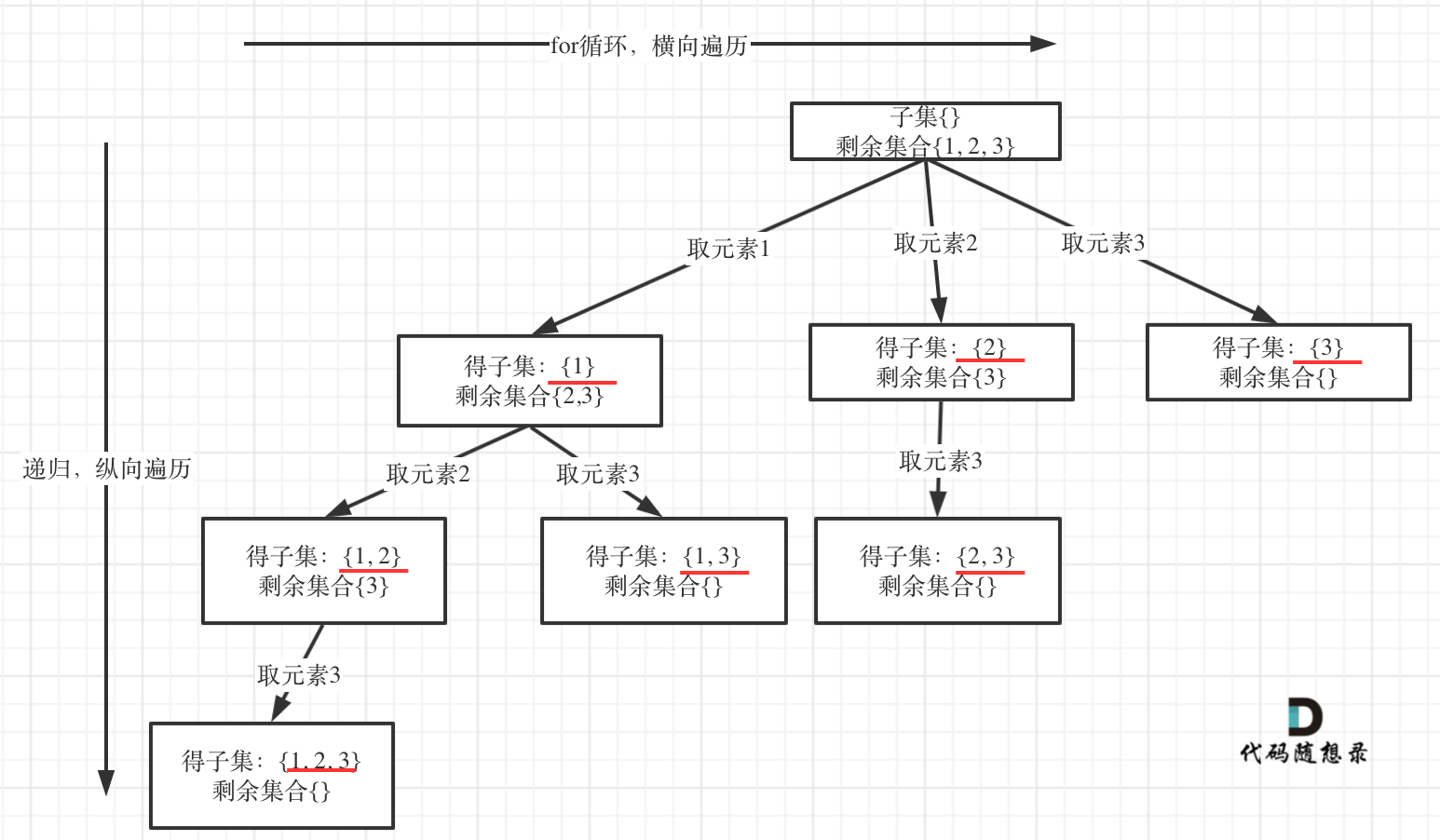
在回溯算法:求子集问题!中讲解了子集问题,在树形结构中子集问题是要收集所有节点的结果,而组合问题是收集叶子节点的结果。
如图:
认清这个本质之后,今天的题目就是一道模板题了。
其实可以不需要加终止条件,因为startIndex >= nums.size(),本层for循环本来也结束了,本来我们就要遍历整棵树。
有的同学可能担心不写终止条件会不会无限递归?
并不会,因为每次递归的下一层就是从i+1开始的。
如果要写终止条件,注意:result.push_back(path);要放在终止条件的上面,如下:
result.push_back(path); // 收集子集,要放在终止添加的上面,否则会漏掉自己
if (startIndex >= nums.size()) { // 终止条件可以不加
return;
}
早起的哈希表系列没有总结,所以哈希表:总结篇!(每逢总结必经典)如约而至。
可能之前大家做过很多哈希表的题目,但是没有串成线,总结篇来帮你串成线,捋顺哈希表的整个脉络。
大家对什么时候各种set与map比较疑惑,想深入了解红黑树,哈希之类的。
如果真的只是想清楚什么时候使用各种set与map,不用看那么多,把关于哈希表,你该了解这些!看了就够了。
本周我们依次介绍了组合问题,分割问题以及子集问题,子集问题还没有讲完,下周还会继续。
我讲解每一种问题,都会和其他问题作对比,做分析,所以只要跟着细心琢磨相信对回溯又有新的认识。
最近这两天题目有点难度,刚刚开始学回溯算法的话,按照现在这个每天一题的速度来,确实有点快,学起来吃力非常正常,这些题目都是我当初学了好几个月才整明白的,哈哈。
所以大家能跟上的话,已经很优秀了!
还有一些录友会很关心leetcode上的耗时统计。
这个是很不准确的,相同的代码多提交几次,大家就知道怎么回事了。
leetcode上的计时应该是以4ms为单位,有的多提交几次,多个4ms就多击败50%,所以比较夸张,如果程序运行是几百ms的级别,可以看看leetcode上的耗时,因为它的误差10几ms对最终影响不大。
所以我的题解基本不会写击败百分之多少多少,没啥意义,时间复杂度分析清楚了就可以了,至于回溯算法不用分析时间复杂度了,都是一样的爆搜,就看谁剪枝厉害了。
一些录友表示最近回溯算法看的实在是有点懵,回溯算法确实是晦涩难懂,可能视频的话更直观一些,我最近应该会在B站(同名:「代码随想录」)出回溯算法的视频,大家也可以看视频在回顾一波。
就酱,又是充实的一周,做好本周总结,迎接下一周,冲!