Now that we know what a wallet actually is, how do we actually generate one? First we generate a private key, which is simply a 64 character hexadecimal string. This represents a number between the range 0 and 2^256 (1.15792089e77). From this number, the rest of the “Account” information is derived. For our purposes an account will consist of your Private Key, WIF (Wallet Import Format), public key, and address.
This random source can technically be generated from any source of entropy, but it SHOULD be generated through some form of cryptographic number generation. Most modern programming languages support some form of Private Key Generation via a secure random function available in a standard library.
The first real challenge of any wallet software is deriving all of the account information from the generated private key. Let's go into detail on how each piece of information is derived.
The WIF is relatively easy to understand. In practice, a private key can end up looking something like this:
0C28FCA386C7A227600B2FE50B7CAEEC86D3BF1FBE471BE89827E19D72AA1D
It would be nice to have something that is a bit more human-readable, so we can convert the private key into the WIF, otherwise known as the wallet import format:
5HueCGU8rMjxEXxiPuD5BDku4MkFqeZyd4dZ1jvhTVqvbTLvyTJ
Although this is still not entirely readable, it is certainly better than the original string. The WIF also has some basic error checking, so that when you send to an address denominated by WIF format, you are more likely to catch an error. The conversion from the raw private key to the WIF format was done via a Base58 check encoding algorithm.
Base58 is similar to the common Base64 encoding scheme, except that it removes non-alphanumeric characters as well as characters that might look similar to each other to the human eye. For example 0 (zero), O (capital o), I (capital i) and l (lower case L) are all omitted from the Base58 encoding scheme. The full list of available characters in NEO's Base58 encoding is:
123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz
A full implementation of NEO's check encoding (written in Go) can be seen below:
func b58checkencode(ver uint8, b []byte) (s string) {
/* Prepend version */
bcpy := append([]byte{ver}, b...)
/* Create a new SHA256 context */
sha256_h := sha256.New()
/* SHA256 Hash #1 */
sha256_h.Reset()
sha256_h.Write(bcpy)
hash1 := sha256_h.Sum(nil)
/* SHA256 Hash #2 */
sha256_h.Reset()
sha256_h.Write(hash1)
hash2 := sha256_h.Sum(nil)
/* Append first four bytes of hash */
bcpy = append(bcpy, hash2[0:4]...)
/* Encode base58 string */
s = b58encode(bcpy)
/* For number of leading 0's in bytes, prepend 1 */
for _, v := range bcpy {
if v != 0 {
break
}
s = "1" + s
}
return s
}The steps to perform the check encoding can be broken down as follows:
- Prepend the version byte
- Double hash the resulting hex using SHA256
- Append the first four bytes of the hash to the prepended version
- Convert the hex with prepended version and appended checksum to Base58
- If there any leading zeros in the bytes, attach 1
So to go from the original private key described above to the WIF format we can use this simple function:
// ToWIF converts a NEO private key to a Wallet Import Format string.
func (priv *PrivateKey) ToWIF() (wif string) {
/* See https://en.bitcoin.it/wiki/Wallet_import_format */
/* Convert the private key to bytes */
priv_bytes := priv.ToBytes()
/* Convert bytes to base-58 check encoded string with version 0x80 */
wif = b58checkencode(0x80, priv_bytes)
return wif
}We can see that WIF is an encoding algorithm of the private key which provides basic error checking, and improves human readability by encoding it into Base58 and attaching a version and checksum.
Generally cryptocurrencies use the form of cryptography called Elliptic-curve cryptography. It is used to derive public key from private key whilst being computationally infeasible to do the opposite.
The form of elliptic curve equation is the following: y^2 = x^3 + ax + b
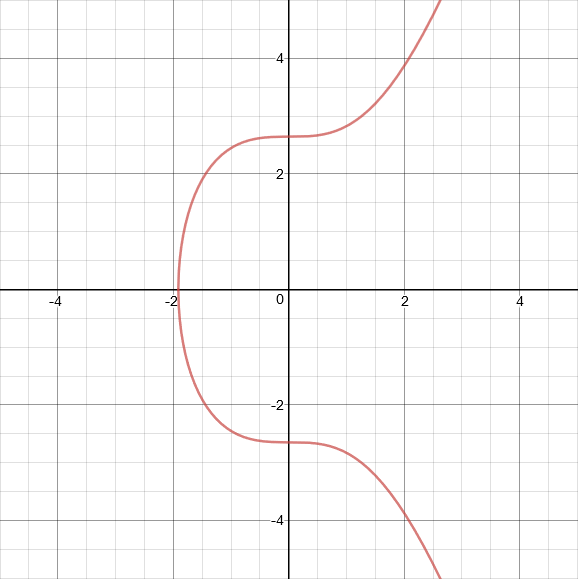
Bitcoin uses an elliptic curve called secp256k1, while NEO uses secp256r1, where k -- means Koblitz and r -- means Random. Essentially, secp256k1's parameters were chosen in a way that allows more efficient calculation (for a very small security trade-off), while secp256r1's parameters were chosen randomly.
The secp256k1 equation is: y^2 = x^3 + 7
The secp256r1 equation is: y^2 = x^3 - 3x + b, where b is 41058363725152142129326129780047268409114441015993725554835256314039467401291
Because of the large b used in secp256r1, below we will use secp256k1 for explanation, but in principle it is the same.
This is what the secp256k1 curve looks like:
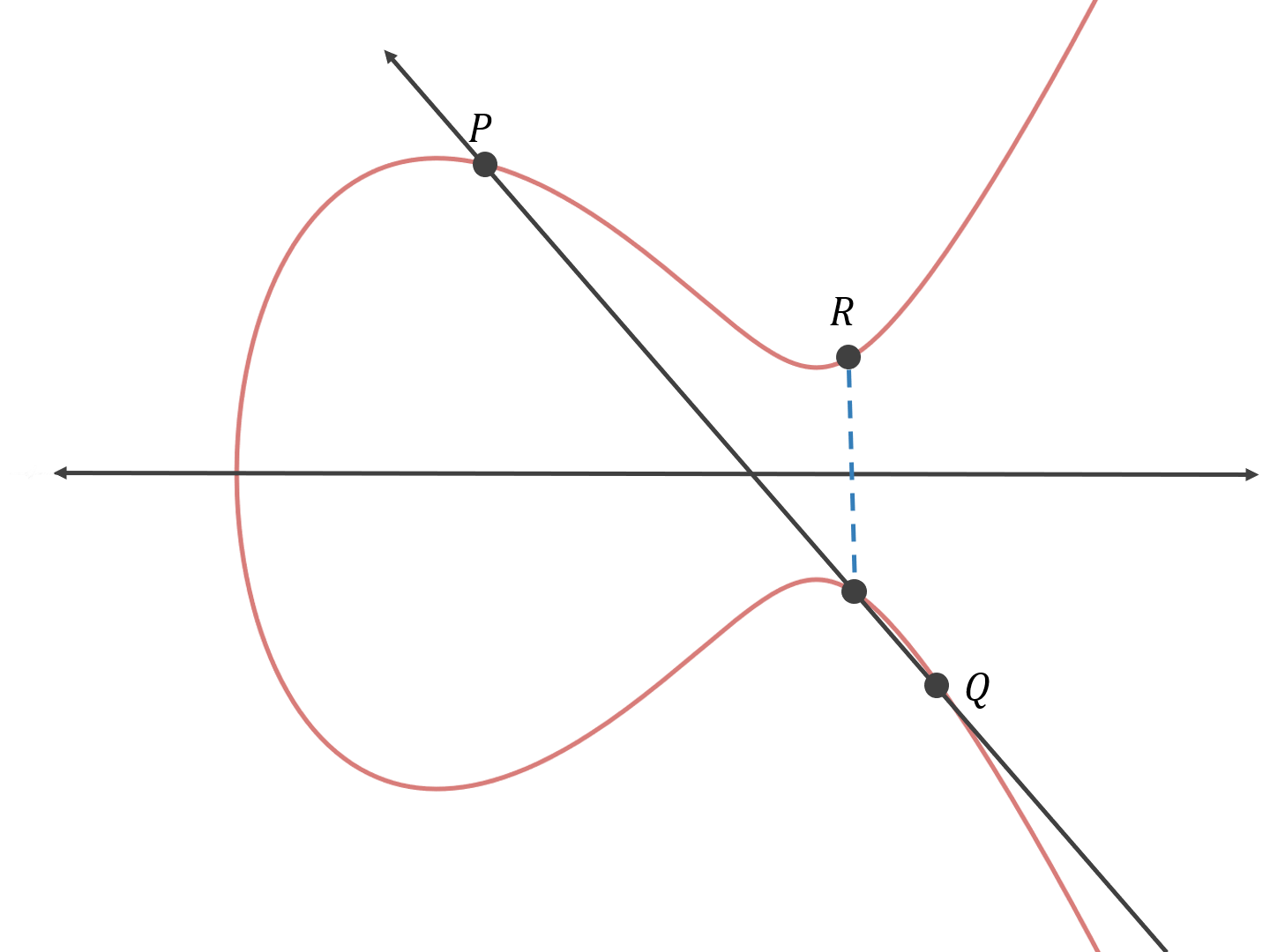
Firstly we'll explain how to do point addition on an elliptic curve.
Having points P and Q, we draw a line that goes through both of them, and find the third point on the intersection of the curve and the line. Then we reflect that point across the x-axis to get R.
P + Q = R
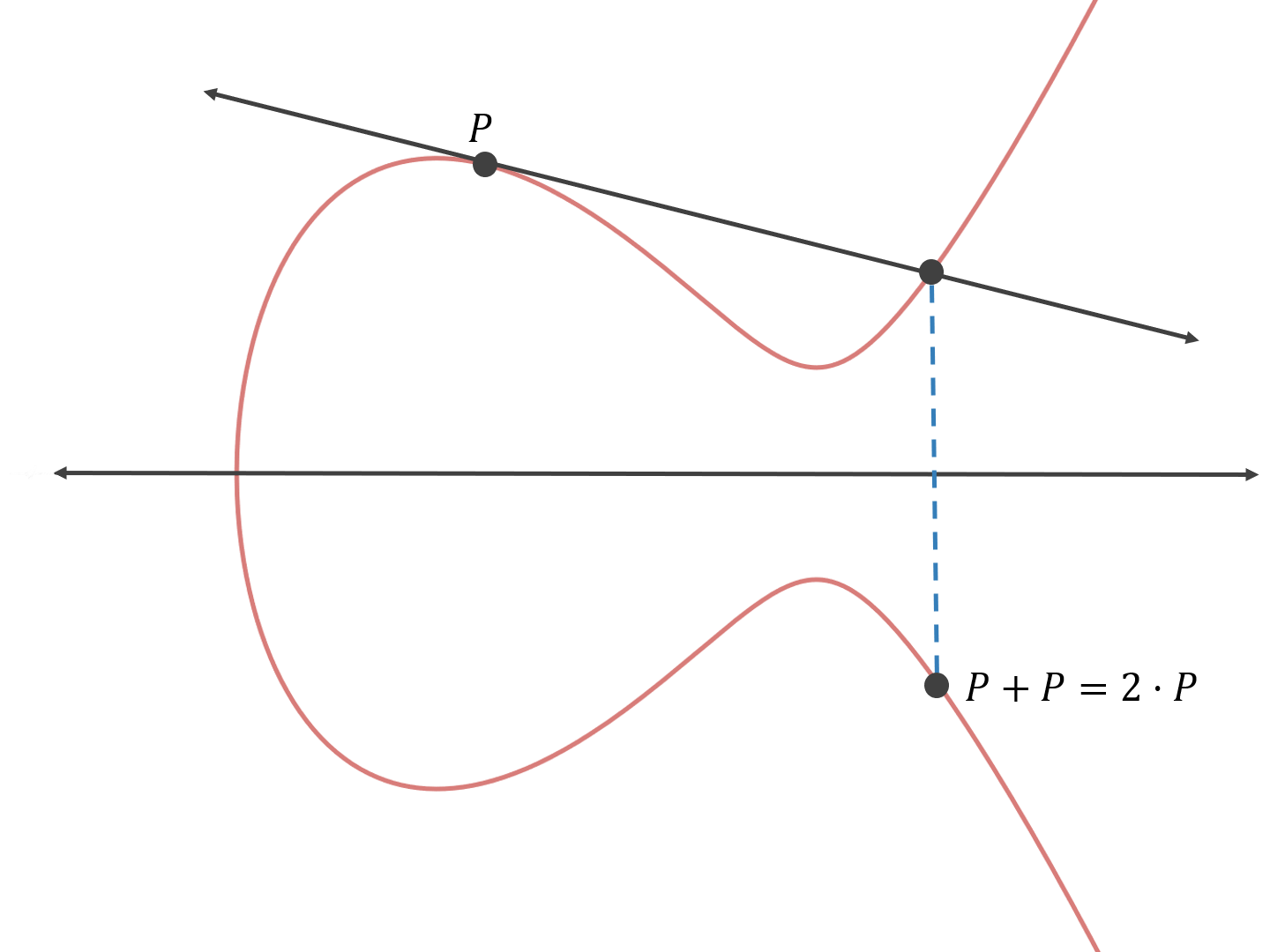
But in elliptic cryptography, rather than adding two arbitrary points together, we add the specified base point on the curve to itself.
We draw a line tangent to the curve at the point P, then apply the same rules as above.
P + P = 2 * P
Remember that the private key is a 256-bit number? Basically, the public key is the result of P adding to itself x times, where x is our private key.
X = x * P, where X is the public key.
To do the opposite (figure out x from X and P) we would need to keep adding P to itself until we get X, which would, on average, make us do 2^128 point additions to figure out x, which is computationally infeasible.
Elliptic Curve Digital Signature Algorithm (ECDSA) is a simulation of Digital Signature Algorithm (DSA) by ECC algorithm. Its advantages include fast speed, reliable strength, and a short signature.
The brief steps are as follows:
Assume private key, public key, and base point as k, K, and G respectively. We know that K = k * G according to the ECC algorithm.
- Select random number r and compute point r * G(x, y).
- Compute s = (h + k * x) / r according to random number r, message M's hash value h, private key k.
- Send message M and signature {r * G, s} to receiver.
- Receiver receives message M and signature {r * G(x, y), s}.
- Compute hash h according to received message.
- Compute h * G / s + x * K / s with sender public key K and compare with r * G. Verification succeeds if both are the same.
A NEO address is generated from the address script, which defines who can spend a transaction output.
Usually the script used is of the form:
PUSHBYTES21 opcode (0x21) + compressed public key (33 bytes) + CHECKSIG opcode (0xAC), meaning the output could be spent only by the owner of the private key for the specified public key.
To calculate a NEO address from transaction script:
- Calculate SHA-256 hash of transaction script
- Calculate RIPEMD-160 hash of the previous output (this is known as the script hash)
- Use Base58 check to encode previous output with the version 0x17 (meaning result will start with A)
Below you will find example code to generate a NEO address from a public key:
// ToNeoAddress converts a NEO public key to a NEO address string.
func (pub *PublicKey) ToNeoAddress() (address string) {
/* Convert the public key to bytes */
pub_bytes := pub.ToBytes()
pub_bytes = append([]byte{0x21}, pub_bytes...)
pub_bytes = append(pub_bytes, 0xAC)
/* SHA256 Hash */
sha256_h := sha256.New()
sha256_h.Reset()
sha256_h.Write(pub_bytes)
pub_hash_1 := sha256_h.Sum(nil)
/* RIPEMD-160 Hash */
ripemd160_h := ripemd160.New()
ripemd160_h.Reset()
ripemd160_h.Write(pub_hash_1)
pub_hash_2 := ripemd160_h.Sum(nil)
program_hash := pub_hash_2
/* Convert hash bytes to base58 check encoded sequence */
address = B58checkencodeNEO(0x17, program_hash)
return address
}The script hash is typically used in smart contracts as the public identifier, as opposed to the address. Since the use of byte arrays is common, it makes a lot more sense as the Base58 encoded versions is meant to be read by humans, not computers!